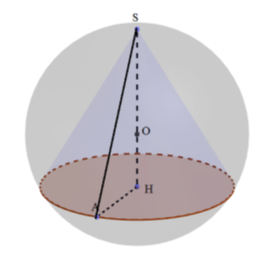
Cho mặt cầu tâm O, bán kính \(R = a\). Một hình nón có đỉnh là ở trên mặt cầu và đáy
38
30/04/2024
Cho mặt cầu tâm O, bán kính \(R = a\). Một hình nón có đỉnh là ở trên mặt cầu và đáy là đường tròn giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho \(SH = \frac{{3a}}{2}\). Độ dài đường sinh l của hình nón bằng:
A. \(l = a\)
B. \(l = a\sqrt 3 \)
C. \(l = a\sqrt 2 \)
Trả lời
Đáp án B
Phương pháp: \(l = \sqrt {{h^2} + {r^2}} \)
Cách giải:
\(SH = \frac{{3a}}{2} > r \Rightarrow OH = SH - r = \frac{{3a}}{2} - a = \frac{a}{2}\)
\(\Delta AOH\) vuông tại H \( \Rightarrow AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta SAH\) vuông tại H \( \Rightarrow SA = \sqrt {S{H^2} + A{H^2}} = \sqrt {{{\left( {\frac{{3a}}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = a\sqrt 3 \)
\( \Rightarrow l = a\sqrt 3 \)