Cho mặt cầu (S) có bán kính R, hình trụ (H) có đường tròn hai đáy thuộc (S) và có chiều cao
46
02/05/2024
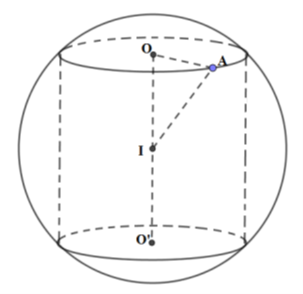
Cho mặt cầu (S) có bán kính R, hình trụ (H) có đường tròn hai đáy thuộc (S) và có chiều cao \(h = \frac{{2R}}{{\sqrt 3 }}\). Tính tỉ số thể tích \({V_1}\) của (H) và \({V_2}\) của (S).
A. \(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{3}\)
B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{9}{{16}}\)
C. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\sqrt 3 }}{3}\)
D. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{\sqrt 3 }}{8}\)
Trả lời
Đáp án C
Phương pháp:
Thể tích khối trụ: \(V = \pi {r^2}h\)
Thể tích khối cầu: \(V = \frac{4}{3}\pi {R^3}\)
Cách giải:
Thể tích khối cầu: \({V_2} = \frac{4}{3}\pi {R^3}\)
Tam giác OIA vuông tại O \( \Rightarrow OA = \sqrt {I{A^2} - O{I^2}} = \sqrt {{R^2} - {{\left( {\frac{R}{{\sqrt 3 }}} \right)}^2}} = \frac{{R\sqrt 6 }}{3}\)
Thể tích khối trụ: \({V_1} = \pi {r^2}h = \pi .\left( {\frac{{R\sqrt 6 }}{3}} \right).\frac{{2R}}{{\sqrt 3 }} = \frac{{4\sqrt 3 \pi {R^3}}}{9}\)
\( \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{{4\sqrt 3 \pi {R^3}}}{9}}}{{\frac{4}{3}\pi {R^3}}} = \frac{{\sqrt 3 }}{3}\)