Cho lăng trụ đứng (ABC.A'B'C') có đáy là tam giác đều cạnh (a). Mặt phẳng ( AB'C') tạo với mặt đáy góc 60^0. Tính theo (a) thể tích lăng trụ ABC.A'B'C' A. 3a^3 căn bậc hai của 3/8 B. 3a
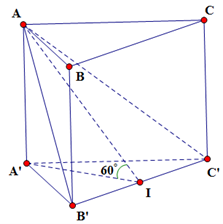
Cho lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Mặt phẳng \(\left( {AB'C'} \right)\) tạo với mặt đáy góc \(60^\circ \). Tính theo \(a\) thể tích lăng trụ \(ABC.A'B'C'\).
A. \(\frac{{3{a^3}\sqrt 3 }}{8}\).
B. \(\frac{{3{a^3}\sqrt 3 }}{4}\).
C. \(\frac{{{a^3}\sqrt 3 }}{8}\).
D. \(\frac{{{a^3}\sqrt 3 }}{2}\).