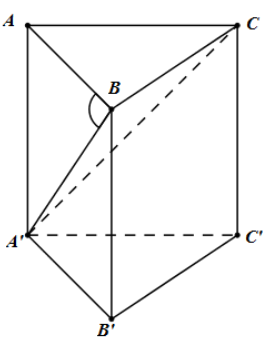
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, \(AB = a,\,\,BC = a\sqrt 2 \), mặt \(\left( {A'BC} \right)\) hợp với đáy \(\left( {ABC} \right)\) một góc \({30^0}\). Tính thể tích V của khối lăng trụ đó?

D. \(V = \frac{{{a^3}\sqrt 6 }}{6}\)

Đáp án C

Phương pháp:

+) Đặt \(AA' = x\), chứng minh tam giác AB’C’ vuông tại B’

+) Xác định góc giữa hai mặt phẳng (AB’C’) và (A’B’C’)

+) Tính AA’. Tính thể tích khối lăng trụ.

Cách giải:

Xét tam giác vuông ABC có \(BC = \sqrt {A{C^2} - A{B^2}} = a\)

Đặt \(AA' = x\) ta có:

\(A'B = \sqrt {{x^2} + {a^2}} \)

\(A'C = \sqrt {{x^2} + 2{a^2}} \)

Xét tam giác A’BC có

\(A'{B^2} + B{C^2} = {x^2} + {a^2} + {a^2} = {x^2} + 2{a^2} = A'{C^2}\)

\( \Rightarrow \Delta A'BC\) vuông tại B.

Ta có: \(\left\{ \begin{array}{l}\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\\\left( {A'BC} \right) \supset A'B \bot BC\\\left( {ABC} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \left( {A'BC} \right);\left( {ABC} \right) = \left( {AB;A'B} \right) \Rightarrow ABA' = {30^0}\)

Xét tam giác vuông AA’B có: \(AA' = AB.tan{30^0} = \frac{a}{{\sqrt 3 }}\)

Vậy \(V{ & _{ABC.A'B'C'}} = AA'.{S_{ABC}} = \frac{a}{{\sqrt 3 }}.\frac{1}{2}{a^2} = \frac{{{a^3}\sqrt 3 }}{6}\)