Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên là 3a / 2. Tính số đo góc tạo
29
01/05/2024
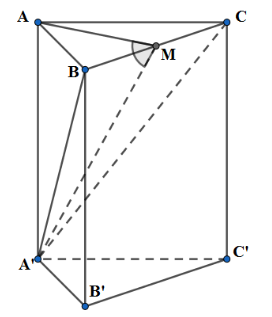
Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên là \(\frac{{3a}}{2}\). Tính số đo góc tạo bởi hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\)
A. \({60^0}\)
B. \({30^0}\)
C. \({45^0}\)
Trả lời
Đáp án A
Phương pháp:
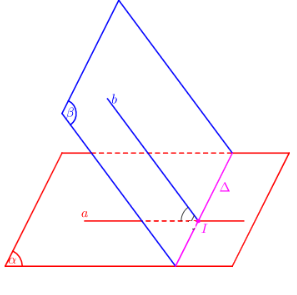
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của\(\left( \alpha \right),\,\left( \beta \right)\) .
- Xác định 1 mặt phẳng\(\left( \gamma \right) \bot \Delta \) .
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),\,\,b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\left( \beta \right):\,\,\left( {\left( \alpha \right);\left( \beta \right)} \right) = \left( {a;b} \right)\)
Cách giải:
Gọi M là trung điểm của BC. Khi đó, \(AM \bot BC\) (do \(\Delta ABC\) đều)
Mà \(BC \bot AA' \Rightarrow BC \bot \left( {AMA'} \right)\)
\( \Rightarrow \left( {\left( {ABC} \right);\left( {A'BC} \right)} \right) = \left( {AM,A'M} \right) = AMA'\)
\(\Delta ABC\) đều, cạn bằng a \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2}\)
\(\Delta AMA'\) vuông tại A
\( \Rightarrow \tan AMA' = \frac{{AA'}}{{AM}} = \frac{{\frac{{3a}}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \sqrt 3 \Rightarrow AMA' = {60^0}\)
\( \Rightarrow \left( {\left( {ABC} \right),\left( {A'BC} \right)} \right) = {60^0}\)