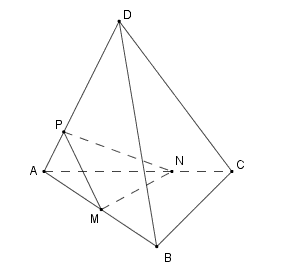
Cho khối tứ diện ABCD có thể tích bằng V. Gọi M là trung điểm cạnh AB, N thuộc cạnh AC sao cho AN = 2NC, P thuộc cạnh AD sao cho PD = 3AP. Thể tích của
Cho khối tứ diện \[ABCD\] có thể tích bằng \(V\). Gọi \(M\) là trung điểm cạnh \(AB\), \(N\) thuộc cạnh \(AC\) sao cho \(AN = 2NC\), \(P\) thuộc cạnh \(AD\) sao cho \(PD = 3AP\). Thể tích của khối đa diện \(MNP.BCD\) tính theo \(V\) là
A. \(\frac{{21}}{{24}}V\).
B. \(\frac{5}{6}V\).
C. \(\frac{7}{8}V\).
D. \(\frac{{11}}{{12}}V\).
