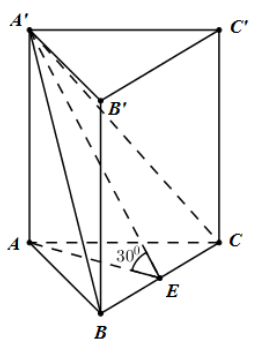
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều. Mặt phẳng $\left( {A'BC} \right)$ tạo với đáy góc ${30^0}$ và tam giác A’BC có diện tích bằng $8{a^2}$. Tính thể tích V của khối lăng trụ đã cho.

D. $V = 16\sqrt 3 {a^3}$

Đáp án A

Phương pháp:

+) Xác định góc giữa hai mặt phẳng (A’BC) và (ABC).

+) Đặt $AB = x$, tính diện tích tam giác A’BC theo x, từ đó tìm x.

+) ${V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}}$

Cách giải: Gọi E là trung điểm của BC ta có:

$\left\{ \begin{array}{l}AE \bot BC\\AA' \bot BC\end{array} \right. \Rightarrow BC \bot \left( {AA'E} \right) \Rightarrow BC \bot A'E$

$\Rightarrow \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \left( {A'E;AE} \right) = A'EA = {30^0}$

Đặt $AB = x$ ta có: $AE = \frac{{x\sqrt 3 }}{2}$

$\Rightarrow \cos {30^0} = \frac{{AE}}{{A'E}} \Rightarrow A'E = \frac{{AE}}{{\cos {{30}^0}}} = x$

${S_{\Delta A'BC}} = \frac{1}{2}A'E.BC = \frac{1}{2}{x^2} = 8{a^2} \Leftrightarrow {x^2} = 16{a^2} \Leftrightarrow a = 4a$

$\Rightarrow {S_{\Delta ABC}} = \frac{{{{\left( {4a} \right)}^2}\sqrt 3 }}{4} = 4\sqrt 3 {a^2}$