Cho khối lăng trụ ABC.A'B'C' có thể tích bằng 2020. Gọi M,N lần lượt là trung điểm của AA'; BB'và điểm P nằm trên cạnh CC' sao cho PC = 3PC'. Thể tích của khối đa diện lồi có các đỉnh là các
54
26/04/2024
Cho khối lăng trụ ABC.A′B′C′ có thể tích bằng 2020. Gọi M,N lần lượt là trung điểm của AA′; BB′và điểm P nằm trên cạnh CC′sao cho PC=3PC′. Thể tích của khối đa diện lồi có các đỉnh là các điểm A,B,C,M,N,P bằng
A. 20203.
B. 53533.
C. 25253.
D. 35353.
Trả lời
Lời giải
Giả sử V=VABC.A′B′C′=2020.
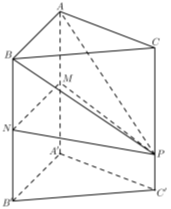
Cách 1
Ta có VC′.ABC=13d(C′;(ABC)).SΔABC=V3⇒VC′.ABB′A′=23V.
Lại có VP.ABCVC′.ABC=13.d(P;(ABC)).SΔABC13.d(C′;(ABC)).SΔABC=d(P;(ABC))d(C′;(ABC))=PCCC′=34⇒VP.ABC=14V.
Ta có \frac{{{V_{P.ABNM}}}}{{{V_{C'.ABB'A'}}}} = & \frac{{\frac{1}{3}.d\left( {P;\left( {ABB'A'} \right)} \right).{S_{ABNM}}}}{{\frac{1}{3}.d\left( {C;\left( {ABB'A'} \right)} \right).{S_{ABB'A'}}}}.
Mà d(P;(ABB′A′))=d(C;(ABB′A′))và SABNM=12SABB′A′.
Suy ra VP.ABNMVC′.ABB′A′=12⇒VP.ABNM=13V.
Vậy VABC.MNP=VP.ABNM+VP.ABC=712V=35353.
Cách 2: Dùng công thức giải nhanh
Ta có: VABC.MNPVABC.A′B′C′=13(AMAA′+BNBB′+CPCC′)⇒VABC.MNP=20203(12+12+34)=35353.

