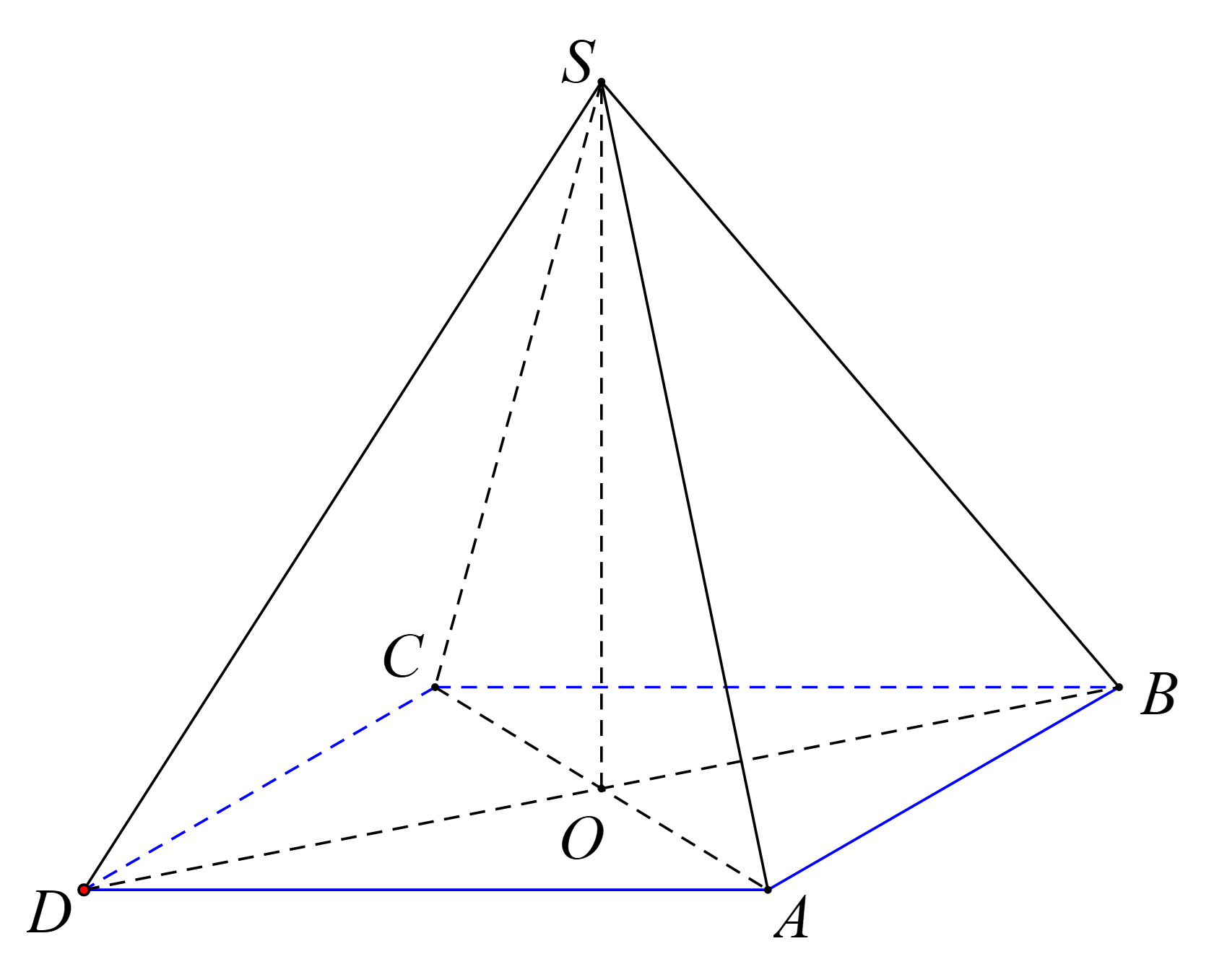
Cho khối chóp tứ giác đều S.ABCD có cạnh bên bằng 6, góc giữa đường thẳng SA và BC bằng 60^0. Tính thể tích V của khối chóp S.ABCD. A. V = 36 B. V = 18 C. V = 36 căn bậc hai của 2
Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh bên bằng \(6\), góc giữa đường thẳng \(SA\) và \(BC\) bằng \(60^\circ \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
A. \(V = 36\).
B. \(V = 18\).
C. \(V = 36\sqrt 2 \).
D. \(V = 18\sqrt 3 \).