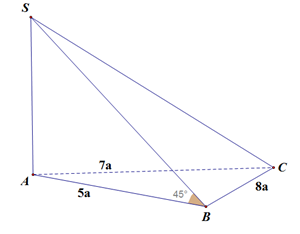
Cho khối chóp tam giác S.ABC có SA ( ABC), tam giác ABC có độ dài 3 cạnh là AB = 5a; BC = 8a; AC = 7a, góc giữa SB và ( ABC) là 45^0. Tính thể tích khối chóp S.ABC A. 50 căn bậc hai của 3
Cho khối chóp tam giác \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) có độ dài \(3\) cạnh là \(AB = 5a\); \(BC = 8a\); \(AC = 7a\), góc giữa \(SB\) và \(\left( {ABC} \right)\) là \(45^\circ \). Tính thể tích khối chóp \(S.ABC\).
A. \(50\sqrt 3 {a^3}\).
B. \(\frac{{50\sqrt 3 }}{3}{a^3}\).
C. \(\frac{{50}}{3}{a^3}\).
D. \(\frac{{50\sqrt 7 }}{3}{a^3}\).