Cho khối chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M và N theo thứ tự là trung điểm của SA và SB. Tính k = VS.CDMN/VBCNADM? A. k = 1/2. B. k = 3/5. C. k = 5/8 D. k = 3/8
32
26/04/2024
Cho khối chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\) và \(N\) theo thứ tự là trung điểm của \(SA\) và \(SB\). Tính \(k = \frac{{{V_{S.CDMN}}}}{{{V_{BCNADM}}}}\)?
A. \(k = \frac{1}{2}\).
B. \(k = \frac{3}{5}\).
C. \(k = \frac{5}{8}\).
D. \(k = \frac{3}{8}\).
Trả lời
Lời giải
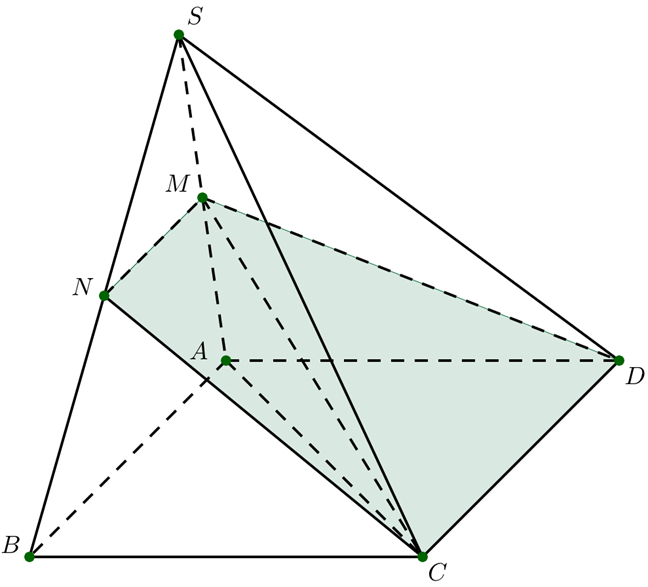
▪ Ta có: \(\frac{{{V_{S.MNC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SC}}{{SC}} = \frac{1}{4}\)\( \Rightarrow \frac{{{V_{S.MNC}}}}{{\frac{1}{2}{V_{S.CDAB}}}} = \frac{1}{4}\)\( \Rightarrow \frac{{{V_{S.MNC}}}}{{{V_{S.CDAB}}}} = \frac{1}{8}\)
▪ Và: \(\frac{{{V_{S.MCD}}}}{{{V_{S.ACD}}}} = \frac{{SM}}{{SA}}.\frac{{SD}}{{SD}}.\frac{{SC}}{{SC}} = \frac{1}{2}\)\( \Rightarrow \frac{{{V_{S.MCD}}}}{{\frac{1}{2}{V_{S.CDAB}}}} = \frac{1}{2}\)\( \Rightarrow \frac{{{V_{S.MCD}}}}{{{V_{S.CDAB}}}} = \frac{1}{4}\).
▪ Suy ra: \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}} = \frac{{{V_{S.MNC}} + {V_{S.MCD}}}}{{{V_{S.CDAB}}}} = \frac{{{V_{S.MNC}}}}{{{V_{S.CDAB}}}} + \frac{{{V_{S.MCD}}}}{{{V_{S.CDAB}}}}\)\( = \frac{1}{8} + \frac{1}{4} = \frac{3}{8}\).
▪ Khi đó: \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}} = \frac{3}{8} \Leftrightarrow \frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}} - {V_{S.CDMN}}}} = \frac{3}{{8 - 3}} = \frac{3}{5}\)
▪ Vậy: \(k = \frac{{{V_{S.CDMN}}}}{{{V_{BCNADM}}}} = \frac{3}{5}\).

