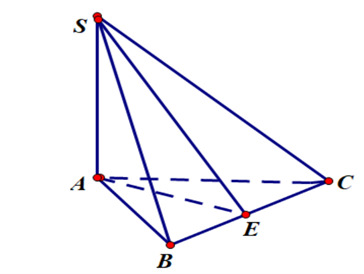
Cho khối chóp (S.ABC) có đáy (ABC)là tam giác vuông cân tại A với BC = 2a. Biết SA vuông góc với đáy, mặt phẳng ( SBC) hợp với đáy ( ABC) một góc 30^0. Thể tích (V)của khối chóp (S.ABC)là
14
04/05/2024
Cho khối chóp \(S.ABC\) có đáy \(ABC\)là tam giác vuông cân tại\(A\) với \(BC = 2a\). Biết \(SA\)vuông góc với đáy, mặt phẳng\(\left( {SBC} \right)\)hợp với đáy\(\left( {ABC} \right)\) một góc \({30^0}\). Thể tích \(V\)của khối chóp \(S.ABC\)là
A. \(V = \frac{{2\sqrt 3 {a^3}}}{3}\).
B. \(V = \frac{{\sqrt 3 {a^3}}}{3}\).
C. \(V = \frac{{\sqrt 3 {a^3}}}{9}\).
D. \(V = \frac{{2\sqrt 3 {a^3}}}{9}\).
Trả lời
Lời giải
Chọn C
Gọi \(E\) là trung điểm \(BC\)
Ta có :\(AE \bot BC \Rightarrow BC \bot SE\) ( Vì \(AE\) là hình chiếu vuông góc \(SE\) trên mặt phẳng\(\left( {ABC} \right)\))
\( \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \)\(\widehat {SEA} = {30^0}\)
\(SA = \tan {30^0}.AE = \tan {30^0}.\frac{1}{2}BC = \frac{{\sqrt 3 }}{3}.\frac{1}{2}.2a = \frac{{\sqrt 3 }}{3}a\)
\(AB = AC = \frac{{BC}}{{\sqrt 2 }} = \sqrt 2 a\)
Thể tích \(V\)của khối chóp \(S.ABC\)là:\(V = \frac{1}{3}.SA.{S_{ABC}} = \frac{1}{3}.\frac{{\sqrt 3 }}{3}a.\frac{1}{2}{\left( {\sqrt 2 a} \right)^2} = \frac{{\sqrt 3 {a^3}}}{9}\).
