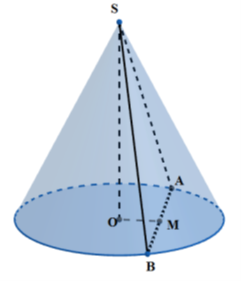
Cho hình nón đỉnh S có đường cao bằng 6cm, bán kính đáy bằng 10cm. Trên đường tròn đáy lấy hai điểm A, B sao cho \(AB = 12cm\). Diện tích tam giác bằng:

D. \(60\,c{m^2}\)

Đáp án D

Phương pháp:

+) Gọi M là trung điểm của AB, O là tâm của đường tròn đáy \( \Rightarrow OM \bot AB\)

+) Tính AB, SM, \({S_{\Delta SAB}} = \frac{1}{2}SM.AB\)

Gọi M là trung điểm của AB, O là tâm của đường tròn đáy \( \Rightarrow OM \bot AB\)

\(\Delta OMB\) vuông tại M \( \Rightarrow OM = \sqrt {O{B^2} - M{B^2}} = \sqrt {{{10}^2} - {{\left( {\frac{{12}}{2}} \right)}^2}} = 8\left( {cm} \right)\)

\(\Delta OMS\) vuông tại O \( \Rightarrow SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {{6^2} + {8^2}} = 10\left( {cm} \right)\)

Ta có: \(AB \bot SO,\,\,AB \bot OM \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot SM\)