Cho hình lập phương ABCD.A'B'C'D', khoảng cách từ C' đến mặt phẳng ( A'BD) bằng 4a căn bậc hai của 3 /3. Tính theo a thể tích khối lập phương ABCD.A'B'C'D' A. V = 8a^3 B. V = 3 căn bậc ha
79
26/04/2024
Cho hình lập phương \(ABCD.A'B'C'D'\), khoảng cách từ \(C'\) đến mặt phẳng \(\left( {A'BD} \right)\) bằng \(\frac{{4a\sqrt 3 }}{3}.\) Tính theo \(a\) thể tích khối lập phương \(ABCD.A'B'C'D'\,.\)
A. \(V = 8{a^3}.\)
B. \(V = 3\sqrt 3 {a^3}.\)
C. \(V = 8\sqrt 3 {a^3}.\)
D. \(V = 216{a^2}.\)
Trả lời
Lời giải
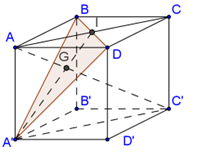
Gọi \(I\) là giao điểm của \(AC\) và \(BD.\)
Trong mặt phẳng \(\left( {ACC'A'} \right)\)\(AC'\) cắt \(A'I\) tại \(G.\)
Do \(AI\)song song \(A'C'\) và \(AI = \frac{1}{2}AC'\) nên \(IG = \frac{1}{2}GA'.\)
Suy ra \(G\) là trọng tâm tam giác \(A'BD\), mà tam giác \(A'BD\) đều (có các cạnh là các đường chéo của những hình vuông bằng nhau) nên \(GA' = GB = GD\) và \(AA' = AB = AD\) suy ra \(AG \bot (A'BD).\)
Do đó khoảng cách từ \(C'\)đến mặt phẳng \(\left( {A'BD} \right)\) là \(C'G.\)
Mặt khác \(C'G = \frac{2}{3}AC' = \frac{2}{3}AB\sqrt 3 = \frac{{4a\sqrt 3 }}{3} \Rightarrow AB = 2a.\) Vậy \(V = 8{a^3}.\)

