Cho hình lăng trụ S.ABCD có đáy là tam giác đều cạnh $2a\sqrt{2}$  và $A\text{'}A=a\sqrt{3}$ . Hình chiếu vuông góc của điểm A' trên mặt phẳng $\left(ABC\right)$  trùng với trọng tâm G của tam giác BC. Tính thể tích V của khối lăng trụ đã cho.

A. $V=\frac{a^3}{2}$ . 

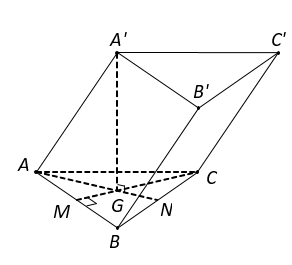
Gọi $M,N$  lần lượt là trung điểm $AB,BC$ .

Khi đó $G=AN\cap CM$  là trọng tâm $\Delta ABC.$

Theo giả thiết, ta có $A\text{'}G\perp \left(ABC\right)$ .

Tam giác $ABC$  đều cạnh $2a\sqrt{2}$  nên suy ra

      $AN=a\sqrt{6}\stackrel{}{\to }AG=\frac{2}{3}AN=\frac{2}{3}a\sqrt{6}.$

Tam giác vuông A'GA, có $A\text{'}G=\sqrt{A\text{'}{A}^2-A{G}^2}=\frac{a\sqrt{3}}{3}.$

Diện tích tam giác ABC là $S_{\Delta ABC}={\left(2a\sqrt{2}\right)}^2.\frac{\sqrt{3}}{4}=2a^2\sqrt{3}.$

Vậy thể tích khối lăng trụ $V_{ABC.A\text{'}B\text{'}C\text{'}}=S_{ABC}.A\text{'}G=2a^3.$  Chọn D.