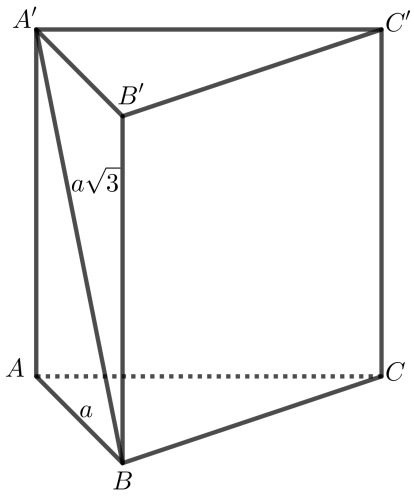
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại B, AB = a và A'B = a căn bậc hai của 3. Thể tích khối lăng trụ ABC.A'B'C' bằng: A. a^3 căn bậc hai của 3 /2 B. a^/6 C. a
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(B\),\(AB = a\) và \(A'B = a\sqrt 3 \). Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
A. \(\frac{{{a^3}\sqrt 3 }}{2}\)
B. \(\frac{{{a^3}}}{6}\)
C. \(\frac{{{a^3}}}{2}\)
D. \(\frac{{{a^3}\sqrt 2 }}{2}\)