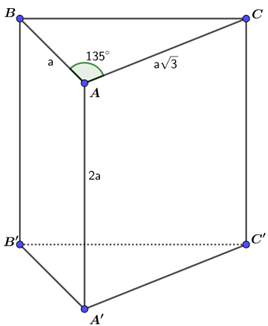
Cho hình lăng trụ đứng ABC.A'B'C'. Biết AA' = 2a, AB = a, AC = a căn bậc hai của 3, góc BAC = 135^0. Tính thể tích của khối lăng trụ ABC.A'B'C'? A. 3a^3/2 B. a^3. căn bậc hai của 6 /3
Cho hình lăng trụ đứng \(ABC.A'B'C'\). Biết \[AA' = 2a\,,\,AB = a\,,\,AC = a\sqrt 3 \], \(\widehat {{\rm{BAC}}} = {135^0}\). Tính thể tích của khối lăng trụ \(ABC.A'B'C'\)?
A. \(\frac{{3{a^3}}}{2}\).
B. \(\frac{{{a^3}.\sqrt 6 }}{3}\).
C. \(\frac{{{a^3}.\sqrt 6 }}{2}\).
D. \(\frac{{{a^3}.\sqrt 6 }}{6}\).
