Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a căn bậc hai của 3 /3. Đường thẳng BC' tạo với mặt phẳng ( ACC'A') góc alpha thỏa mãn alpha = 2. Thể tích khối lăng trụ ABC.A'B'C' bằng
59
28/04/2024
Cho hình lăng trụ đều \[ABC.A'B'C'\]có cạnh đáy bằng \[\frac{{2a\sqrt 3 }}{3}\]. Đường thẳng \[BC'\] tạo với mặt phẳng \[\left( {ACC'A'} \right)\] góc \[\alpha \] thỏa mãn \[\cot \alpha = 2\]. Thể tích khối lăng trụ \[ABC.A'B'C'\] bằng
A. \[\frac{4}{3}{a^3}\sqrt {11} \].
B. \[\frac{1}{9}{a^3}\sqrt {11} \].
C. \[\frac{1}{3}{a^3}\sqrt {11} \].
D. \[\frac{2}{3}{a^3}\sqrt {11} \].
Trả lời
Lời giải
Chọn C
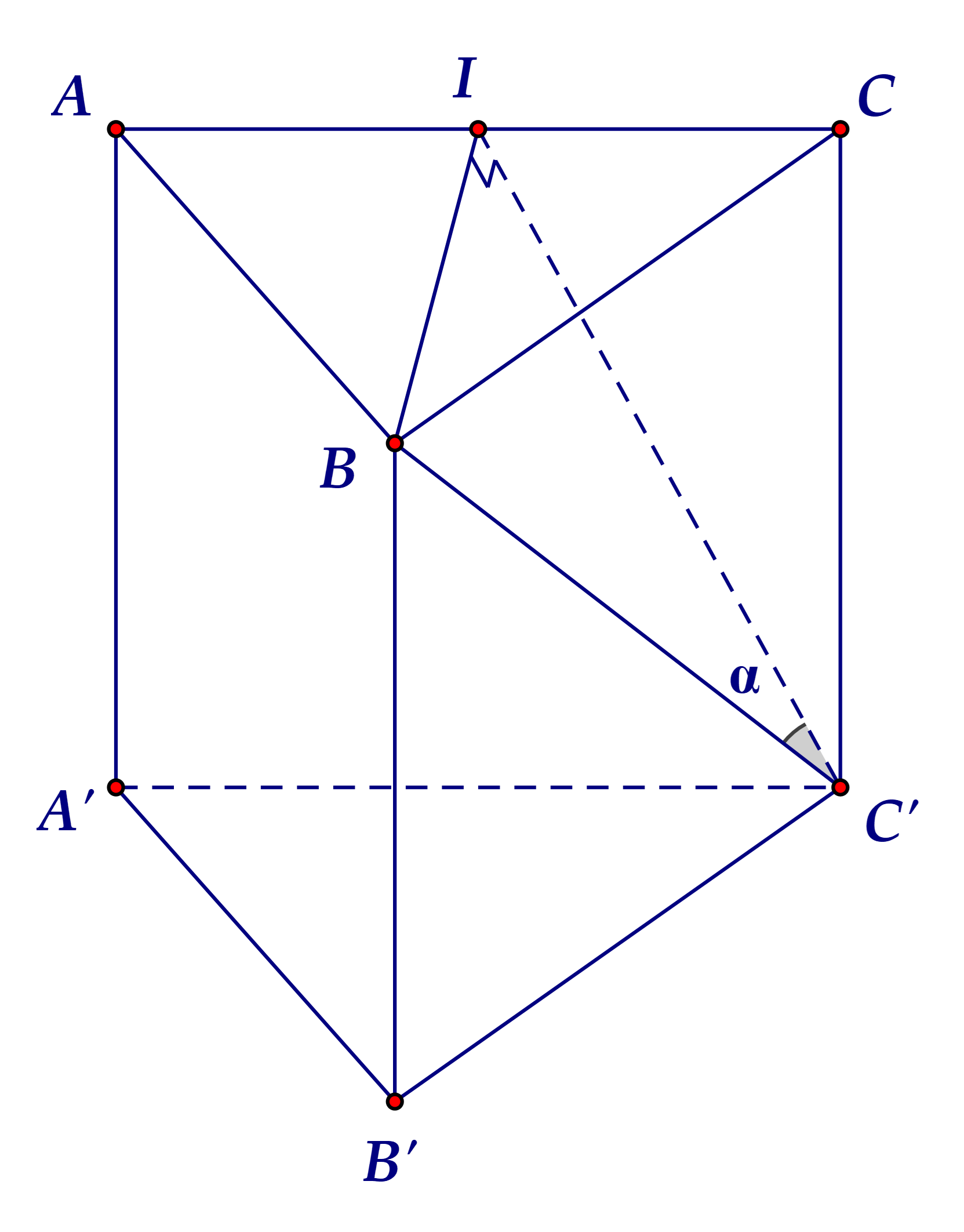
Gọi \[I\] là trung điểm \[AC\], suy ra \[BI \bot AC\].
Mặt khác do \[BI \bot CC'\] nên \[BI \bot \left( {ACC'A'} \right)\].
Do đó \[\alpha = \widehat {\left( {BC',\left( {ACC'A'} \right)} \right)} = \widehat {\left( {BC',IC'} \right)} = \widehat {BC'I}\].
Ta có: \[{S_{\Delta ABC}} = {\left( {\frac{{2a\sqrt 3 }}{3}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{3}\] và \[BI = \frac{{2a\sqrt 3 }}{3}.\frac{{\sqrt 3 }}{2} = a\].
Theo đề bài: \[\cot \alpha = 2 \Leftrightarrow \frac{{C'I}}{{BI}} = 2 \Leftrightarrow C'I = 2a\].
Suy ra \[CC' = \sqrt {C'{I^2} - C{I^2}} = \sqrt {4{a^2} - \frac{{{a^2}}}{3}} = \frac{{a\sqrt {33} }}{3}\].
Vậy thể tích khối lăng trụ \[ABC.A'B'C'\]: \[V = {S_{\Delta ABC}}.CC' = \frac{{{a^2}\sqrt 3 }}{3}.\frac{{a\sqrt {33} }}{3} = \frac{1}{3}{a^3}\sqrt {11} \].
