Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, góc ABC = 60^0 . Chân đường cao hạ từ B’ trùng với tâm O của đáy ABCD; góc giữa mặt phẳng ( BB'C'C) với đáy bằng 60^0. Thể tíc
68
27/04/2024
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy \(ABCD\)là hình thoi cạnh a,\[\widehat {ABC} = {60^0}\] . Chân đường cao hạ từ B’ trùng với tâm O của đáy \(ABCD\); góc giữa mặt phẳng \(\left( {BB'C'C} \right)\) với đáy bằng \({60^0}\). Thể tích lăng trụ bằng:
A. \(\frac{{3{a^3}\sqrt 3 }}{8}\)
B. \(\frac{{2{a^3}\sqrt 3 }}{9}\)
C. \(\frac{{3{a^3}\sqrt 2 }}{8}\)
D. \(\frac{{3{a^3}}}{4}\)
Trả lời
Giải:
Chọn A
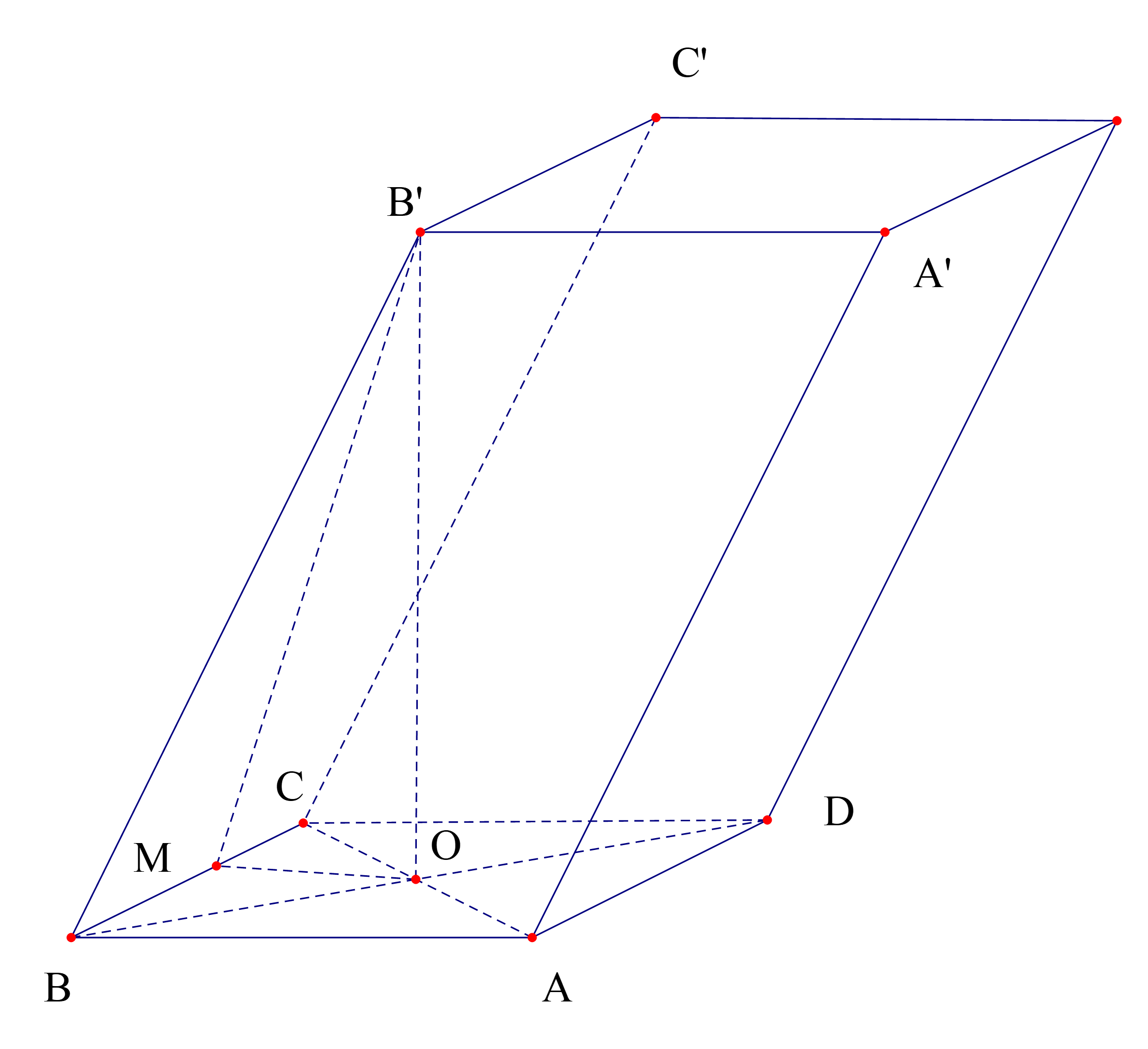
Từ giả thiết suy ra tam giác ABC đều nên \({S_{ABCD}} = 2{S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{2}\)
Gọi M là hình chiếu của O trên BC thì BC vuông góc với mặt phẳng (B’OM). Suy ra góc giữa mặt phẳng (BB’C’C) và mặt phẳng đáy là góc \[\widehat {B'MO} = {60^0}\]
Ta lại có tam giác BOC vuông tại O, có đường cao OM nên
\(\begin{array}{l}\frac{1}{{O{M^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{16}}{{3{a^2}}}\\ \Rightarrow OM = \frac{{a\sqrt 3 }}{4}\end{array}\)
Tam giác B’OM vuông tại O nên
\(\begin{array}{l}B'O = OM\tan {60^0} = \frac{{3a}}{4}\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = B'O.{S_{ABCD}} = \frac{{3a}}{4}.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{3{a^3}\sqrt 3 }}{8}\end{array}\)

