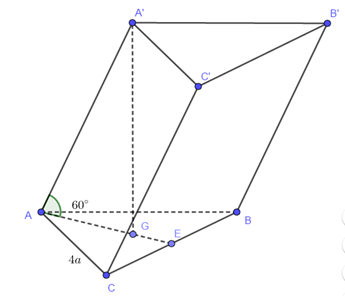
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 4a, hình chiếu của A' trên đáy trùng với trọng tâm G của tam giác ABC, góc giữa cạnh bên và đáy bằng 30^0. Tính thể tích khối lăng trụ
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(4a\), hình chiếu của \(A'\) trên đáy trùng với trọng tâm \(G\) của tam giác \(ABC\), góc giữa cạnh bên và đáy bằng \({30^0}\). Tính thể tích khối lăng trụ \(ABC.A'B'C'\)
A. \(\frac{{16\sqrt 3 {a^3}}}{3}\).
B. \(16{a^3}\sqrt 3 \).
C.\(\frac{{4\sqrt 3 {a^3}}}{3}\).
D. \(\frac{{4\sqrt 3 {a^3}}}{9}\).
