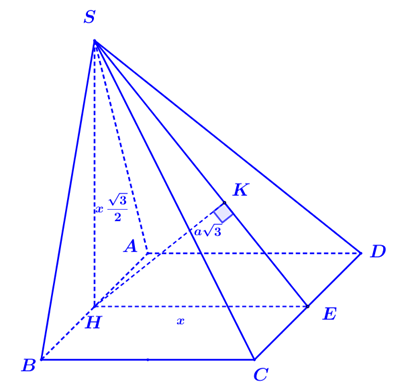
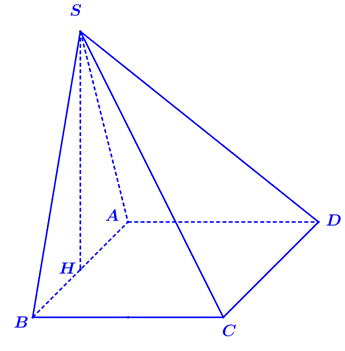
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông, mặt bên ( SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm A đến mặt phẳng ( SCD) bằng a căn bậc hai
Cho hình chóp tứ giác \[S.ABCD\] có đáy là hình vuông, mặt bên \[\left( {SAB} \right)\] là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách từ điểm \[A\] đến mặt phẳng \[\left( {SCD} \right)\] bằng \(a\sqrt 3 \). Tính thể tích \(V\) của khối chóp \(S.ABCD\).
A. \(V = \frac{{7{a^3}\sqrt {21} }}{6}\).
B. \(V = \frac{{7{a^3}\sqrt {21} }}{2}\).
C. \(V = \frac{{7{a^3}\sqrt 7 }}{6}\).
D. \(V = \frac{{3{a^3}\sqrt 7 }}{2}\).