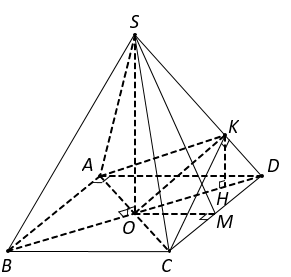
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2a.
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh 2a. Mặt bên tạo với đáy góc 600 . Gọi K là hình chiếu vuông góc của O trên SD. Tính theo a thể tích V của khối tứ diện DKAC.
A. V=2a3√315 .
B. V=4a3√35 .
C. V=4a3√315 .
D. V=a3√3 .