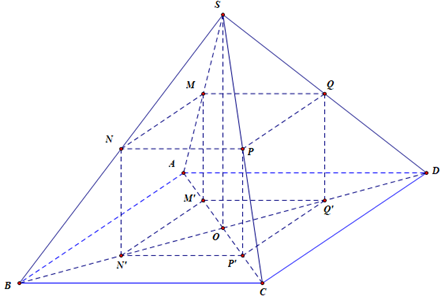
Cho hình chóp tứ giác đều S.ABCD có tâm đáy là O. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Hình hộp có đáy là MNPQ, đáy kia là M'N'P'Q' với M' là trung điểm của AO. Gọi V1 là
Cho hình chóp tứ giác đều \(S.ABCD\) có tâm đáy là \(O\). Gọi \(M,\,N,\,P,\,Q\) lần lượt là trung điểm của \(SA,\,SB,\,SC,\,SD\). Hình hộp có đáy là \(MNPQ\), đáy kia là \(M'N'P'Q'\) với \(M'\) là trung điểm của \(AO\). Gọi \({V_1}\) là thể tích khối chóp \(S.ABCD\), \({V_2}\) là thể tích khối hộp \(MNPQ.M'N'P'Q'\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\)
A. \[\frac{5}{8}\].
B. \[\frac{8}{5}\].
C. \[\frac{8}{3}\].
D. \[\frac{3}{8}\].
