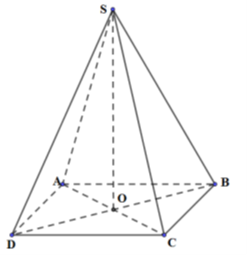
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \(a\sqrt 3 \), góc \(ASB = {60^0}\). Tính thể tích của khối nón đỉnh S có đáy là đường tròn ngoại tiếp tứ giác ABCD.
D. \(\frac{{\pi {a^3}\sqrt 6 }}{2}\)
Đáp án B
Phương pháp: \({V_{n\'o n}} = \frac{1}{3}\pi {R^2}h\)
Cách giải:
S.ABCD là chóp tứ giác đều \( \Rightarrow \) ABCD là hình vuông
\(BD = AB\sqrt 2 = a\sqrt 3 .\sqrt 2 = a\sqrt 6 \Rightarrow r = OB = \frac{{BD}}{2} = \frac{{a\sqrt 6 }}{2}\)
Tam giác SAB có: \(SA = AB,\,\,\,ASB = {60^0} \Rightarrow \Delta ASB\) đều \( \Rightarrow SA = SB = a\sqrt 3 \)
\( \Rightarrow SB = SD = AD = AB = a\sqrt 3 \)
\( \Rightarrow \Delta SBD = ABD\left( {c.c.c} \right) \Rightarrow SO = OA = OB = OD = \frac{{a\sqrt 6 }}{2}\)
Thể tích của khối nón đỉnh S có đáy là đường tròn ngoại tiếp tứ giác ABCD:
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .O{A^2}.SO = \frac{1}{3}\pi .{\left( {\frac{{a\sqrt 6 }}{2}} \right)^3} = \frac{{\pi {a^3}\sqrt 6 }}{4}\)