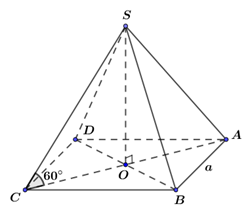
Cho hình chóp tứ giác đều S.ABCD có AB = a, cạnh bên tạo với đáy một góc 60^0. Thể tích khối chóp S.ABC bằng A. a^3 căn bậc hai của 3 /6 B. a^3 căn bậc hai của 3 /12
42
26/04/2024
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), cạnh bên tạo với đáy một góc \(60^\circ \). Thể tích khối chóp \(S.ABC\) bằng
A. \(\frac{{{a^3}\sqrt 3 }}{6}\).
B. \(\frac{{{a^3}\sqrt 3 }}{{12}}\).
C. \(\frac{{{a^3}\sqrt 6 }}{{12}}\).
D. \(\frac{{{a^3}\sqrt 6 }}{6}\).
Trả lời
Lời giải
Gọi \[O = AC \cap BD\] \( \Rightarrow SO \bot \left( {ABCD} \right)\)\( \Rightarrow \left( {\widehat {SC,\left( {ABCD} \right)}} \right) = \left( {\widehat {SC,OC}} \right) = \widehat {SCO} = 60^\circ \).
Xét tam giác \(SOC\) vuông tại \(O\), có \(SO = OC.\tan 60^\circ = \frac{{a\sqrt 2 }}{2}.\sqrt 3 = \frac{{a\sqrt 6 }}{2}\).
Diện tích tam giác \(\Delta ABC\) là \({S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}{a^2}\).
Vậy \({V_{S.ABC}} = \frac{1}{3}SO.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 6 }}{2}.\frac{1}{2}{a^2} = \frac{{{a^3}\sqrt 6 }}{{12}}\).
