Cho hình chóp tam giác đều S.ABC có cạnh đáy AB = 2a căn bậc hai của 3; góc giữa mặt bên và mặt đáy là 60^0. Tính thể tích khối chóp S.ABC A. 8a^3 căn bậc hai của 3 B. a^3 căn bậc hai
34
26/04/2024
Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy \(AB = 2a\sqrt 3 ;\) góc giữa mặt bên và mặt đáy là \(60^\circ .\) Tính thể tích khối chóp \(S.ABC.\)
A. \(8{a^3}\sqrt 3 .\)
B. \({a^3}\sqrt 3 .\)
C. \(3{a^3}.\)
D. \(3{a^3}\sqrt 3 .\)
Trả lời
Lời giải
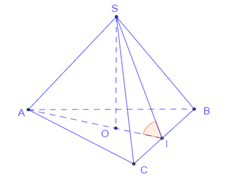
Gọi \(O\) là trọng tâm tam giác \(ABC \Rightarrow SO \bot \left( {ABC} \right).\)
Gọi \(I\) là trung điểm \(BC \Rightarrow OI \bot BC.\)
\( \Rightarrow \widehat {\left( {\left( {SBC} \right),\,\left( {ABC} \right)} \right)} = \widehat {SIO} \Rightarrow \widehat {SIO} = 60^\circ .\)
\( \Rightarrow SO = OI.\tan \widehat {SIO} = \frac{1}{3}.\frac{{2a\sqrt 3 .\sqrt 3 }}{2}.\sqrt 3 = a\sqrt 3 .\)
Ta có \({S_{ABC}} = \frac{{{{\left( {2a\sqrt 3 } \right)}^2}.\sqrt 3 }}{4} = 3{a^2}\sqrt 3 .\)
\( \Rightarrow {V_{S.ABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.a\sqrt 3 .3{a^2}\sqrt 3 = 3{a^3}.\)

