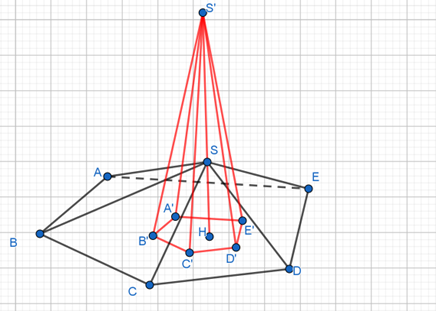
Cho hình chóp S.ABCDE có đáy là hình ngũ giác và có thể tích là V. Nếu tăng chiều cao của hình chóp lên 3 lần đồng thời giảm độ dài các cạnh đi 3 lần thì ta được khối chóp mới S'.A'B'C'D'E' c
Cho hình chóp \[S.ABCDE\] có đáy là hình ngũ giác và có thể tích là \[V\]. Nếu tăng chiều cao của hình chóp lên \[3\] lần đồng thời giảm độ dài các cạnh đi \[3\]lần thì ta được khối chóp mới \[S'.A'B'C'D'E'\] có thể tích là \[V'\]. Tỉ số thể tích \[\frac{{V'}}{V}\] là:
A. \[3\].
B. \(\frac{1}{5}\).
C. \[1\].
D. \[\frac{1}{3}\].