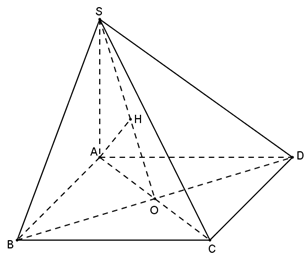
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và SA vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SBD).

Chọn C

Gọi O là giao điểm của AC và BD.

Gọi H là hình chiếu của lên SO.

Ta có $BD\perp AC$ và $BD\perp SA$ nên $BD\perp \left(SAC\right)\Rightarrow BD\perp AH$.

Lại có $AH\perp SO$ và $AH\perp BD$ nên $AH\perp \left(SBD\right)\Rightarrow d\left(A,\left(SBD\right)\right)=AH$.

Trong tam giác ABC có $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}\Rightarrow AO=\frac{a\sqrt{2}}{2}$.

Trong tam giác SAO có $\frac{1}{A{H}^2}=\frac{1}{A{O}^2}+\frac{1}{S{A}^2}=\frac{1}{{\left(\frac{a\sqrt{2}}{2}\right)}^2}+\frac{1}{{\left(2a\right)}^2}=\frac{9}{4a^2}\Rightarrow AH=\frac{2a}{3}$.