Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=SB, SC=SD
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và tổng diện tích hai tam giác SAB và SCD bằng Tính thể tích V của khối chóp S.ABCD
A.
B.
C.
D.
A.
Gọi lần lượt là trung điểm của AB và CD
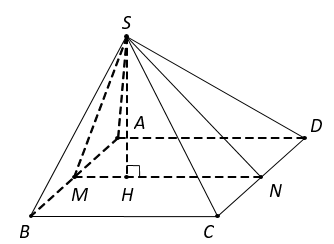
Tam giác SAB cân tại S suy ra với
Vì suy ra và
Kẻ
Ta có
Tam giác SMN vuông tại S nên
Giải hệ
Vậy thể tích khối chóp Chọn C.