Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, đường chéo AC=a, tam giác SAB

9 19/04/2024

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, đường chéo AC=a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, góc giữa $(S C D)$ và đáy bằng $45^{0}$ . Tính theo a thể tích V của khối chóp S.ABCD.

A. $V = \frac{a^{3}}{4}$ .

V = \frac{3 a^{3}}{4}

V = \frac{a^{3}}{2}

D. $V = \frac{a^{3}}{12}$ .

Trả lời

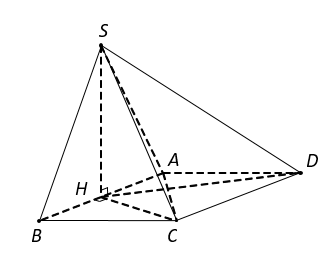
Media VietJack

Gọi H là trung điểm AB, suy ra $S H ⊥ A B$ .

Mà $(S A B) ⊥ (A B C D)$ theo giao tuyến AB nên $S H ⊥ (A B C D)$

Tam giác ABC đều cạnh a nên

\{\begin{cases} C H ⊥ A B \overset{}{\to} C H ⊥ C D \\ C H = \frac{A B \sqrt{3}}{2} = \frac{a \sqrt{3}}{2} \end{cases} .

Ta có $\{\begin{cases} (S C D) \cap (A B C D) = C D \\ S C \subset (S C D), S C ⊥ C D \\ H C \subset (A B C D), H C ⊥ C D \end{cases}$ suy ra

$45^{0} = \hat{(S C D), (A B C D)} = \hat{S C, H C} = \hat{S C H}$

Tam giác vuông SHC, có $S H = H C . \tan \hat{S C H} = \frac{a \sqrt{3}}{2}$ .

Diện tích hình thoi ABCD là $S_{A B C D} = 2 S_{Δ A D C} = \frac{a^{2} \sqrt{3}}{2}$ .

Vậy thể tích khối chóp $V_{S . A B C D} = \frac{1}{3} S_{A B C D} . S H = \frac{a^{3}}{4} .$ Chọn A.

Trắc nghiệm Toán 12 Bài Khái niệm về thể tích khối đa diện có đáp án (Mới nhất)

Xem tất cả

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, đường chéo AC=a, tam giác SAB

Trả lời

Câu hỏi cùng chủ đề

Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O cạnh a góc

Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và

Tính thể tích V của một khối lăng trụ biết đáy có diện tích S=10cm^2 cạnh bên tạo với mặt

Cho hình lăng trụ tam giác ABC có đáy ABC là tam giác vuông cân tại A, cạnh

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh có độ dài bằng 2. Hình chiếu vuông

Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật tâm O và AB=a,

Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 12cm^3. Tính thể tích V của khối tứ diện

Tính thể tích V của khối lăng trụ ABC.A'B'C' biết thể tích khối chóp A.BCB'C' bằng

Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=1; AC=2 cạnh bên

Tính thể tích V của khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A

Danh mục