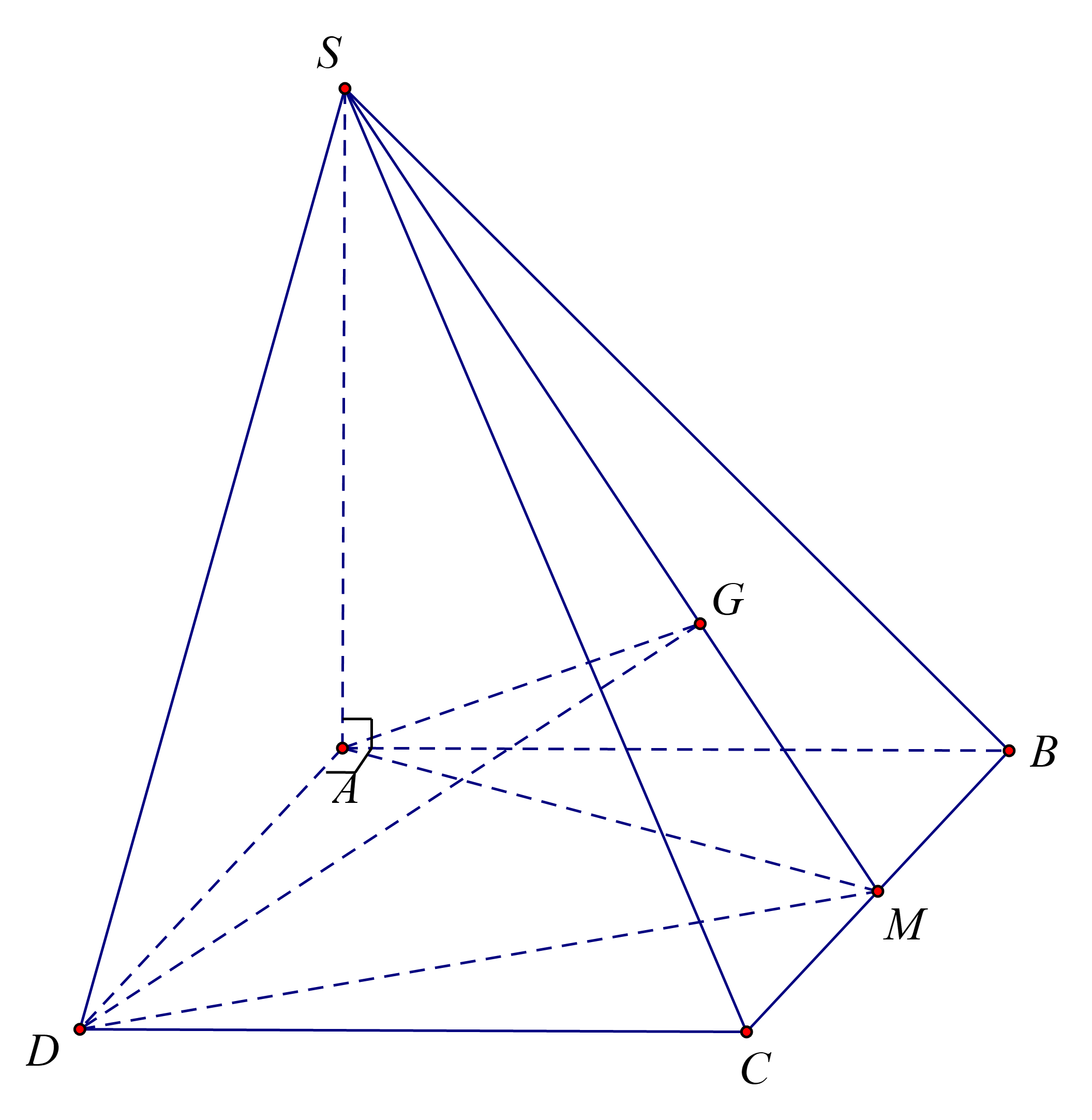
Cho hình chóp S.ABCD có SA ( ABCD), ABCD là hình chữ nhật. SA = AD = 2a. Góc giữa ( SBC) và mặt đáy ( ABCD) là 60^0. Gọi G là trọng tâm tam giác (SBC). Tính thể tích khối chóp (S.AGD) là
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình chữ nhật. \(SA = AD = 2a\). Góc giữa \(\left( {SBC} \right)\) và mặt đáy \(\left( {ABCD} \right)\) là \(60^\circ \). Gọi \(G\) là trọng tâm tam giác \(SBC\). Tính thể tích khối chóp \(S.AGD\) là
A. \(\frac{{32{a^3}\sqrt 3 }}{{27}}\).
B. \(\frac{{8{a^3}\sqrt 3 }}{{27}}\).
C. \(\frac{{4{a^3}\sqrt 3 }}{9}\).
D. \(\frac{{16{a^3}}}{{9\sqrt 3 }}\).