Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a Căn 2. Biết rằng SA = SB = SC = SD, SO = 2.a Căn 2

Bài 1 trang 55 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh $a\sqrt{2}$ . Biết rằng SA = SB = SC = SD, SO = $2a\sqrt{2}$ .

a) Chứng minh rằng SO ⊥ (ABCD).

b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.

Trả lời

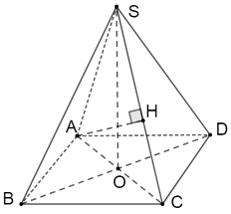
a)Từ giả thiết, dễ dàng nhận thấy ∆SAC và ∆SBD là các tam giác cân.

Ta có: 

Do đó SO ⊥ (ABCD)

b)Ta có: AC = 2a, OC = a, $SC=\sqrt{S{O}^2+O{C}^2}=3a.$

Vẽ đường cao AH của ∆SAC.

Ta có: $AH=\frac{SO.AC}{SC}=\frac{2a\sqrt{2}.2a}{3a}=\frac{4a\sqrt{2}}{3}.$

Vậy độ dài đường cao xuất phát từ đỉnh A của tam giác SAC bằng $\frac{4a\sqrt{2}}{3}$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: