Cho hình chóp S.ABCD có đáy là hình vuông, hình chiếu của S lên (ABCD) là điểm H thuộc cạnh AB thỏa mãn HB = 2HA, góc giữa SC và (ABCD) bằng \({60^0}\). Biết rằng khoảng cách từ A đến (SCD) bằng \(\sqrt {26} \). Thể tích V của khối chóp S.ABCD là

D. \(V = \frac{{128\sqrt {78} }}{3}\)

Đáp án C

Phương pháp:

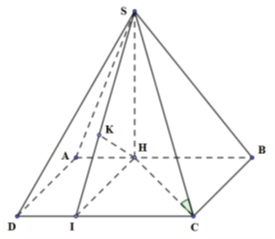
+) \(d\left( {A;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right)\) xác định khoảng cách từ H đến (SCD).

+) Xác định góc giữa SC và mặt đáy.

+) Đặt cạnh của hình vuông ở đáy là x, tính SH và HI theo x.

+) Sử dụng hệ thức lượng trong tam giác vuông để tìm x.

Cách giải:

Do \(AH//\left( {SCD} \right)\) nên \(d\left( {A;\left( {SCD} \right)} \right) = d\left( {H;\left( {SCD} \right)} \right)\)

Kẻ \(HI//AD,\,\,I \in CD,\,\,\,HK \bot SI,\,\,K \in SI\)

\( \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HK = \sqrt {26} \)

Giả sử độ dài cạnh hình vuông ở đáy là x. Khi đó, \(HI = x\)

\(\Delta HBC\) vuông tại B \( \Rightarrow HC = \sqrt {H{B^2} + B{C^2}} = \sqrt {{{\left( {\frac{2}{3}x} \right)}^2} + {x^2}} = \frac{{\sqrt {13} x}}{3}\)

\(SH \bot \left( {ABCD} \right) \Rightarrow \left( {SC;\left( {ABCD} \right)} \right) = \left( {SCH} \right) = {60^0}\)

\(\Delta SHC\) vuông tại H \( \Rightarrow SH = HC.\tan {60^0} = \frac{{\sqrt {13} x}}{3}.\sqrt 3  = \frac{{\sqrt {39} x}}{3}\)

\(\Delta SHI\) vuông tại H,

\(HK \bot SI \Rightarrow \frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{I{H^2}}} \Leftrightarrow \frac{1}{{26}} = \frac{1}{{\frac{{13{x^2}}}{3}}} + \frac{1}{{{x^2}}} = \frac{{16}}{{13{x^2}}} \Leftrightarrow {x^2} = 32 \Rightarrow x = 4\sqrt 2 \)