Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy. Gọi M, N là trung điểm của SA, SB. Mặt phẳng MNCD chia hình chóp đã cho thành hai phần. tỉ số thể tích hai phần S.MNC
54
05/05/2024
Cho hình chóp \(S.ABCD\) có đáy là hình vuông, cạnh bên \(SA\) vuông góc với đáy. Gọi \(M\), \(N\) là trung điểm của \(SA\), \(SB\). Mặt phẳng \(MNCD\) chia hình chóp đã cho thành hai phần. tỉ số thể tích hai phần \(S.MNCD\) và \(MNABCD\) là
A. \(\frac{3}{4}\).
B. \(\frac{3}{5}\).
C. \(\frac{4}{5}\).
D. \(1\).
Trả lời
Lời giải
Chọn B
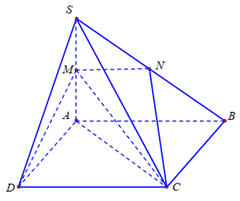
Ta có \({V_{S.ABC}} = {V_{S.ACD}} = \frac{1}{2}{V_{S.ABCD}}\);
và \({V_{S.MNC}} = \frac{{SM}}{{SA}} \cdot \frac{{SN}}{{SB}} \cdot \frac{{SC}}{{SC}} \cdot {V_{S.ABC}} = \frac{1}{4}{V_{S.ABC}}\); \({V_{S.MCD}} = \frac{{SM}}{{SA}} \cdot \frac{{SD}}{{SD}} \cdot \frac{{SC}}{{SC}} \cdot {V_{S.ACD}} = \frac{1}{2}{V_{S.ACD}}\).
Suy ra \({V_{S.MNCD}} = {V_{S.MNC}} + {V_{S.MCD}} = \frac{3}{4}{V_{S.ABC}} = \frac{3}{8}{V_{S.ABCD}}\).
Đồng thời \({V_{MNABCD}} = {V_{S.ABCD}} - {V_{S.MNCD}} = \frac{5}{8}{V_{S.ABCD}}\).
Vậy tỉ số thể tích hai phần \(S.MNCD\) và \(MNABCD\) là \(\frac{3}{5}\).

