Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và $SA=\frac{a\sqrt{6}}{2}$  (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

Đáp án đúng là: C

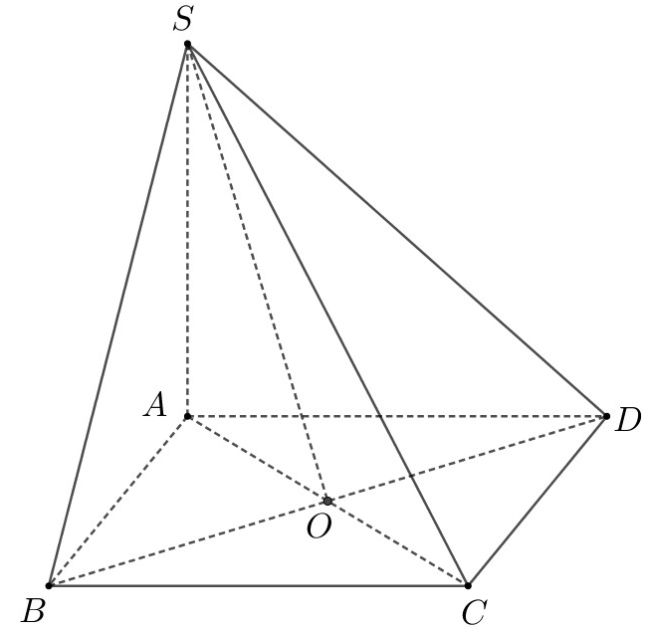
Gọi O là giao điểm của AC và BD. Suy ra $BD\perp AO$ .

Vì $\left\{\begin{array}{l}BD\perp AC\\ BD\perp SA\end{array}\right.\Rightarrow BD\perp \left(SAC\right)$ . Mà $SO\subset \left(SAC\right)$  suy ra $BD\perp SO$ .

Ta có $\left\{\begin{array}{l}BD=\left(SBD\right)\cap \left(ABCD\right)\\ SO\subset \left(SBD\right),SO\perp BD\\ AO\subset \left(ABCD\right),AO\perp BD\end{array}\right.\Rightarrow \left(\widehat{\left(SBD\right),\left(ABCD\right)}\right)=\left(\widehat{SO,AO}\right)=\widehat{SOA}$ .

Vì ABCD là hình vuông cạnh a  nên có $AC=a\sqrt{2}$ ; $AO=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$ .