Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc
39
02/05/2024
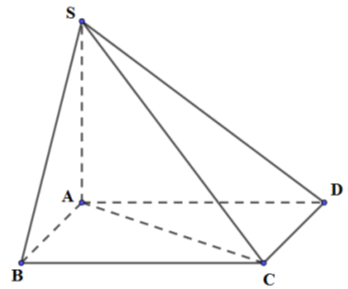
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Các mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy, còn cạnh bên SC tạo với đáy mặt phẳng đáy một góc \({30^0}\). Thể tích của khối chóp đã cho là
A. \(V = \frac{{{a^3}\sqrt 6 }}{9}\)
B. \(V = \frac{{{a^3}\sqrt 6 }}{3}\)
C. \(V = \frac{{{a^3}\sqrt 6 }}{4}\)
D. \(V = \frac{{{a^3}\sqrt 3 }}{9}\)
Trả lời
Đáp án A
Phương pháp:
\({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}}\)
Cách giải:
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {SC;\left( {ABCD} \right)} \right) = \left( {SC;AC} \right) = SCA = {30^0}\)
ABCD có đáy là hình vuông cạnh a \( \Rightarrow AC = a\sqrt 2 \)
Tam giác SAC vuông tại A \( \Rightarrow SA = AC.\tan C = a\sqrt 2 .\tan {30^0} = a\sqrt 2 .\frac{1}{{\sqrt 3 }} = \frac{{a\sqrt 6 }}{3}\)
Thể tích của khối chóp đã cho là: \(V = \frac{1}{3}{S_{ABCD}}.SA = \frac{1}{3}{a^3}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 6 }}{9}\)