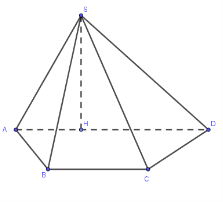
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, \(AB = BC = 2,\,\,AD = 4\); mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng
D. 1
Đáp án C
Phương pháp:
Thể tích khối chóp: \(V = \frac{1}{3}Sh\)
Cách giải:
Kẻ SH vuông góc AB (H thuộc AB). Do mặt bên SAD nằm trong mặt phẳng vuông góc với đáy \( \Rightarrow SH \bot \left( {ABCD} \right)\)
Diện tích tam giác SAD: \({S_{SAD}} = \frac{1}{2}SH.AD = 6 \Rightarrow \frac{1}{2}.SH.4 = 6 \Rightarrow SH = 3\)
Diện tích tam giác BCD: \({S_{BCD}} = \frac{1}{2}.AB.BC = \frac{1}{2}.2.2 = 2\)
Thể tích khối S.BCD: \(V = \frac{1}{3}{S_{BCD}}.SH = \frac{1}{3}.2.3 = 2\)