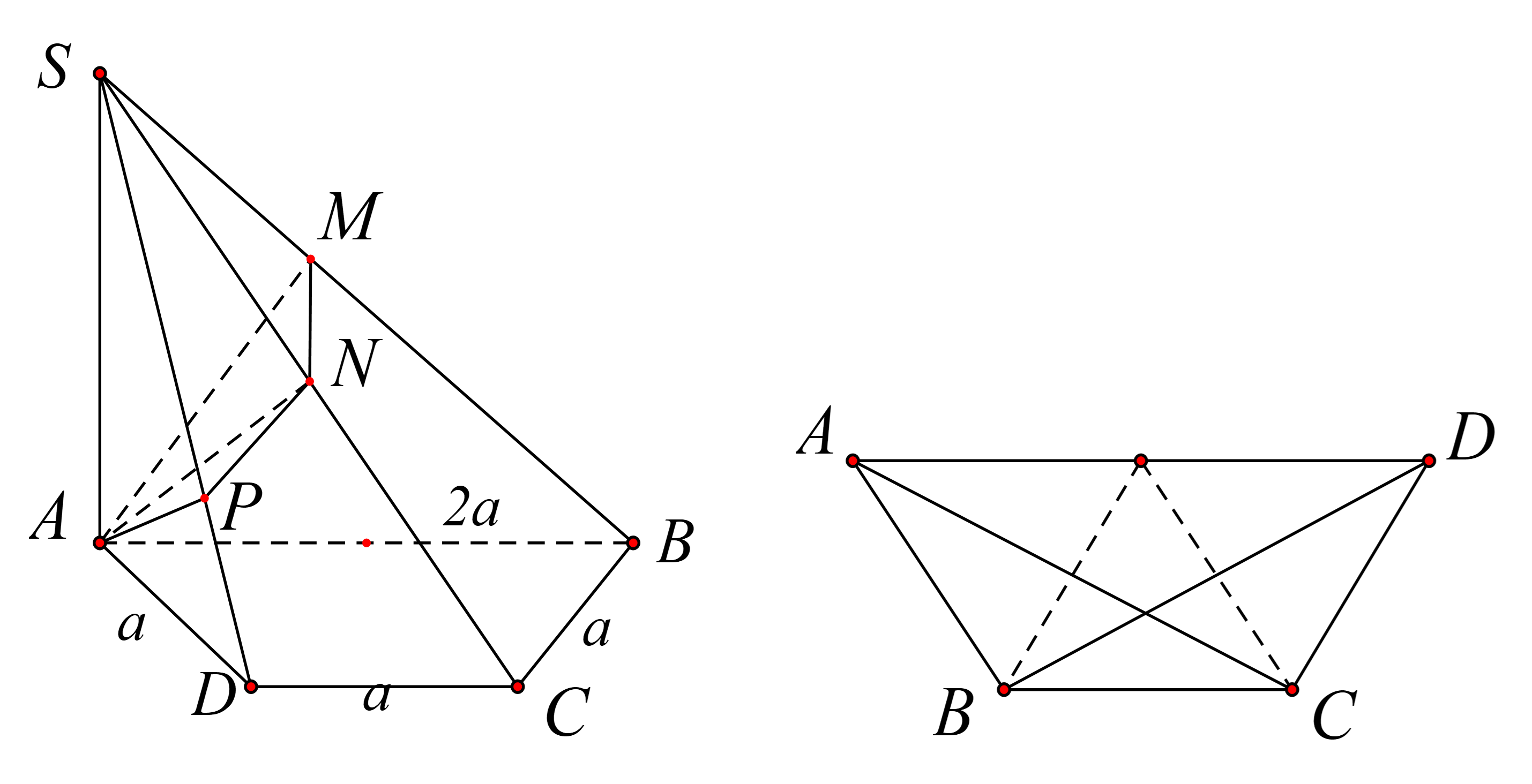
Cho hình chóp S.ABCD có đáy là hình thang cân với AB = 2a; BC = CD = DA = a. SA vuông góc với mặt phẳng đáy, SC tạo với đáy một góc 60^o. Mặt phẳng (P) đi qua (A), vuông góc SB và cắt các cạn
40
26/04/2024
Cho hình chóp \(S.ABCD\) có đáy là hình thang cân với \(AB = 2a;\,BC = CD = DA = a\). \(SA\) vuông góc với mặt phẳng đáy, \(SC\) tạo với đáy một góc \({60^o}\). Mặt phẳng (P) đi qua \(A\), vuông góc \(SB\) và cắt các cạnh \(SB,\,\,SC,\,SD\) lần lượt tại \(M,\,N,\,P\). Tính thể tích khối đa diện \(ABCDMNP\).
A. \(\frac{{668{a^3}\sqrt 3 }}{{2080}}\).
B. \(\frac{{669{a^3}\sqrt 3 }}{{2080}}\).
C. \(\frac{{667{a^3}\sqrt 3 }}{{2080}}\).
D. \(\frac{{666{a^3}\sqrt 3 }}{{2080}}\).
Trả lời
Lời giải
Do là\(ABCD\) hình thang cân\(AB = 2a;\,BC = CD = DA = a\).
Ta có \(AC = DB = a\sqrt 3 \).\(AC \bot BC;\,\,AD \bot DB\).
Do \(\widehat {\left( {SC,(ABCD)} \right)} = \widehat {\left( {SC,AC} \right)} = {60^o}\,\, \Rightarrow SA = 3a\).
Do\(\left( P \right) \bot SB\). Do\(AC \bot BC;\,\,AD \bot DB\) ta chứng minh được \(AM \bot SB\), \(AN \bot SC,\,\,AP \bot SD\).
Có \(\frac{{SM}}{{SB}} = \frac{{S{A^2}}}{{S{B^2}}} = \frac{9}{{13}}\); \(\frac{{SN}}{{SC}} = \frac{{S{A^2}}}{{S{C^2}}} = \frac{3}{4}\); \(\frac{{SP}}{{SD}} = \frac{{S{A^2}}}{{S{D^2}}} = \frac{9}{{10}}\).
Ta tính được \({V_{S.ACD}} = \frac{{{a^3}\sqrt 3 }}{4}\);\({V_{S.ABC}} = \frac{{{a^3}\sqrt 3 }}{2}\).
Có \(\frac{{{V_{SAMN}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}.\frac{{SN}}{{SC}} = \frac{{27}}{{52}}\); \({V_{S.AMN}} = \frac{{27{a^3}\sqrt 3 }}{{104}}\); \(\frac{{{V_{SANP}}}}{{{V_{S.ACD}}}} = \frac{{SP}}{{SD}}.\frac{{SN}}{{SC}} = \frac{{27}}{{40}}\); \({V_{S.ANP}} = \frac{{27{a^3}\sqrt 3 }}{{160}}\).
\[{V_{S.AMNP}} = \frac{{891}}{{2080}}{a^3}\sqrt 3 \]\( \Rightarrow {V_{MNP.ABCD}} = \frac{{669{a^3}\sqrt 3 }}{{2080}}\).
