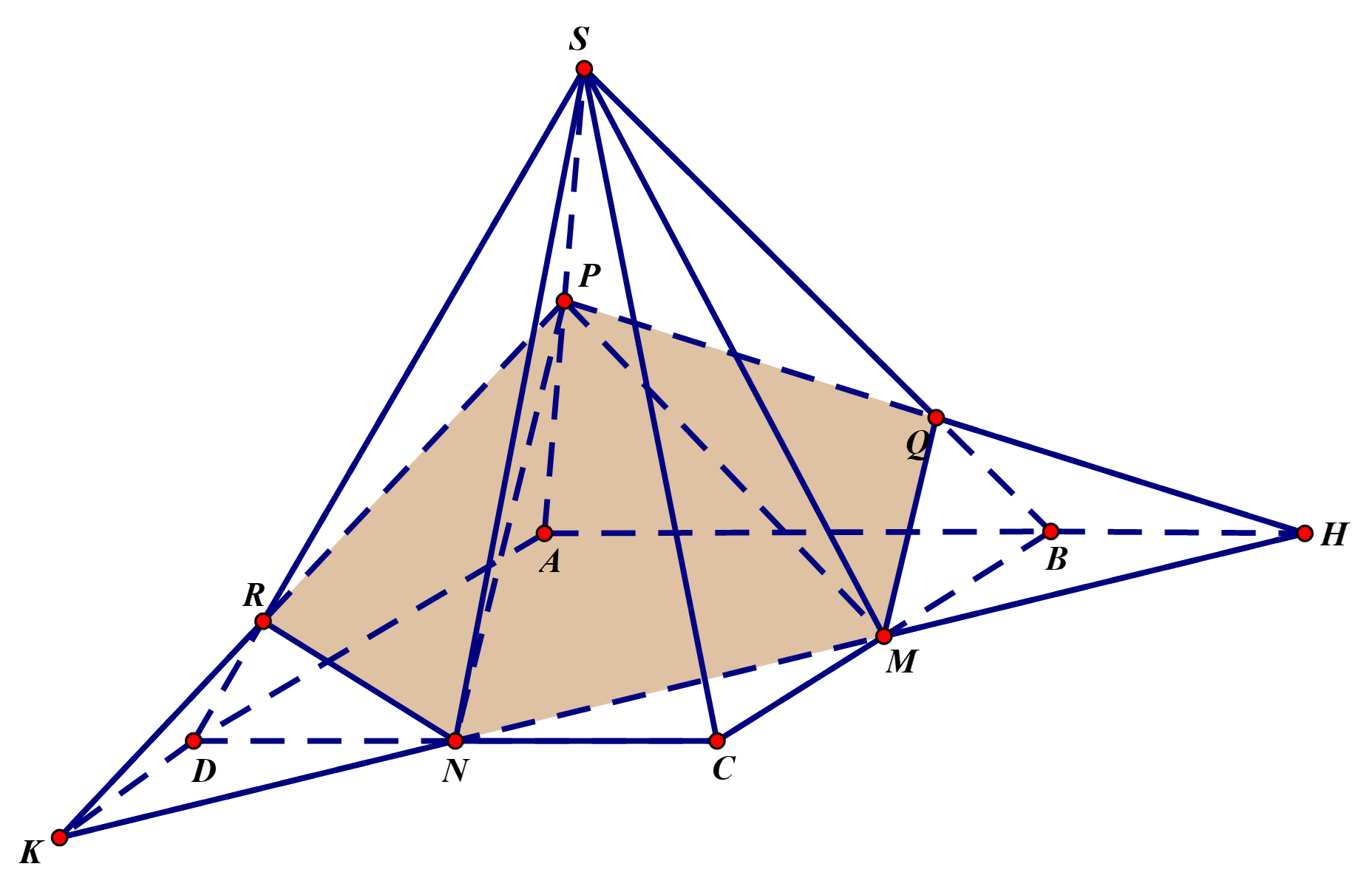
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N và P lần lượt là trung điểm của các đoạn BC, CD và SA. Mặt phẳng ( MNP) chia khối chóp thành hai phần có thể tích lần lượt là V1 và V2.
45
04/05/2024
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\), \(N\) và \(P\) lần lượt là trung điểm của các đoạn \(BC\), \(CD\) và \(SA\). Mặt phẳng \(\left( {MNP} \right)\) chia khối chóp thành hai phần có thể tích lần lượt là \({V_1}\) và \({V_2}\). Biết rằng \({V_1} \le {V_2}\), tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)
A. \(1\).
B. \(\frac{1}{2}\).
C. \(\frac{5}{6}\).
D. \(\frac{2}{3}\).
Trả lời
Lời giải
Chọn A
Ta có \(BH = \frac{1}{3}AH\) suy ra \(B\) là trọng tâm của tam giác \(SAT\).
Do đó, \(\frac{{BQ}}{{BU}} = \frac{{BH}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{BQ}}{{BS}} = \frac{1}{4}\). Tương tự ta có, \(\frac{{DR}}{{SD}} = \frac{1}{4}\).
\(\frac{{{V_{S.PRN}}}}{{{V_{S.ADN}}}} = \frac{{SP}}{{SA}}.\frac{{SR}}{{SD}} = \frac{1}{2}.\frac{3}{4} = \frac{3}{8} \Rightarrow \frac{{{V_{S.PRN}}}}{{{V_{S.ABCD}}}} = \frac{3}{{32}}\).
Tương tự, ta có \(\frac{{{V_{S.PQM}}}}{{{V_{S.ABCD}}}} = \frac{3}{{32}}\).
Lại có \(\frac{{{V_{S.PMN}}}}{{{V_{S.AMN}}}} = \frac{{SP}}{{SA}} = \frac{1}{2} \Rightarrow \frac{{{V_{S.PMN}}}}{{{V_{S.ABCD}}}} = \frac{3}{{16}}\).
\(\frac{{{V_{S.MNC}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\).
Suy ra thể tích khối đa diện chứa đỉnh \(S\) là \({V_1} = \left( {\frac{3}{{32}} + \frac{3}{{32}} + \frac{3}{{16}} + \frac{1}{8}} \right){V_{SABCD}} = \frac{1}{2}{V_{SABCD}}\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = 1\).
