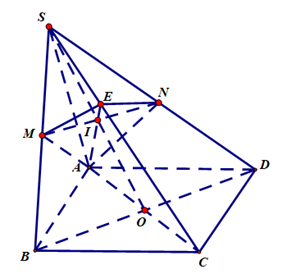
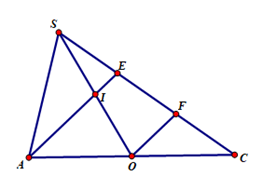
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh (SC) sao cho EC = 2ES, ( alpha ) là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD,
30
04/05/2024
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành và có thể tích \(V\). Gọi \(E\) là điểm trên cạnh \(SC\) sao cho \(EC = 2ES\), \(\left( \alpha \right)\) là mặt phẳng chứa đường thẳng \(AE\) và song song với đường thẳng \(BD\), \(\left( \alpha \right)\) cắt hai cạnh \(SB,\;SD\) lần lượt tại hai điểm \(M,\;N\). Tính theo \(V\) thể tích khối chóp \(S.AMEN\).
A. \(\frac{{2V}}{9}\).
B. \(\frac{V}{3}\).
C. \(\frac{V}{6}\).
D. \(\frac{V}{{12}}\).
Trả lời
Lời giải
Chọn C
Gọi \(O\) là tâm hình bình hành \(ABCD\); \(I\) là giao điểm của \(AE\) và \(SO\).
Theo bài ra: \(\frac{{SE}}{{SC}} = \frac{1}{3}\); \(MN\) đi qua điểm \(I\) và \(MN//BD\).
Ta có: \(\frac{{{V_{S.AME}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SB}}.\frac{{SE}}{{SC}}\); \(\frac{{{V_{S.ANE}}}}{{{V_{S.ADC}}}} = \frac{{SN}}{{SD}}.\frac{{SE}}{{SC}}\), \({V_{S.ABC}} = {V_{S.ADC}} = \frac{V}{2}.\)
Kẻ \(OF//AE,\;\;F \in \left[ {SC} \right]\). Vì \(O\) là trung điểm của \(AC\) nên \(F\) là trung điểm của \(EC\), theo giả thiết suy ra \(E\) là trung điểm của \(SF\).
Xét tam giác \(SOF\) có \(E\) là trung điểm của \(SF\) và \(OF//IE\), suy ra \(I\) là trung điểm của \(SO\).
\( \Rightarrow \frac{{SI}}{{SO}} = \frac{1}{2}\) \( \Rightarrow \frac{{SM}}{{SB}} = \frac{{SN}}{{SD}} = \frac{1}{2}\).
Do đó \(\frac{{{V_{S.AME}}}}{{\frac{1}{2}V}} = \frac{{{V_{S.ANE}}}}{{\frac{1}{2}V}} = \frac{1}{6} \Rightarrow \) \({V_{SAMEN}} = \frac{1}{6}V\).
