Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\) .

Đáp án C

Phương pháp:

Sử dụng công thức tỉ số thể tích cho khối chóp tam giác (Công thức Simson): Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc . Khi đó, \(\frac{{{V_{S.{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \frac{{S{A_1}}}{{SA}}.\frac{{S{B_1}}}{{SB}}.\frac{{S{C_1}}}{{SC}}\)

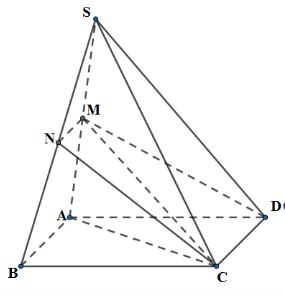
Cách giải:

Gọi V là thể tích khối chóp S.ABCD.

Chia khối chóp S.CDMN làm 2 khối chóp: S.CDM và S.CMN

Ta có: \(\frac{{{V_{S.CDM}}}}{{{V_{S.CDA}}}} = \frac{{SM}}{{SA}} = \frac{1}{2} \Rightarrow {V_{S.CDM}} = \frac{1}{2}{V_{S.CDA}} = \frac{1}{2}.\frac{1}{2}V = \frac{1}{4}V\)

\(\frac{{{V_{S.CMN}}}}{{{V_{S.CAB}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4} \Rightarrow {V_{S.CDM}} = \frac{1}{4}{V_{S.CAB}} = \frac{1}{4}.\frac{1}{2}V = \frac{1}{8}V\)

\( \Rightarrow {V_{S.CDMN}} = \frac{1}{4}V + \frac{1}{8}V = \frac{3}{8}V \Rightarrow \frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}} = \frac{3}{8}\)