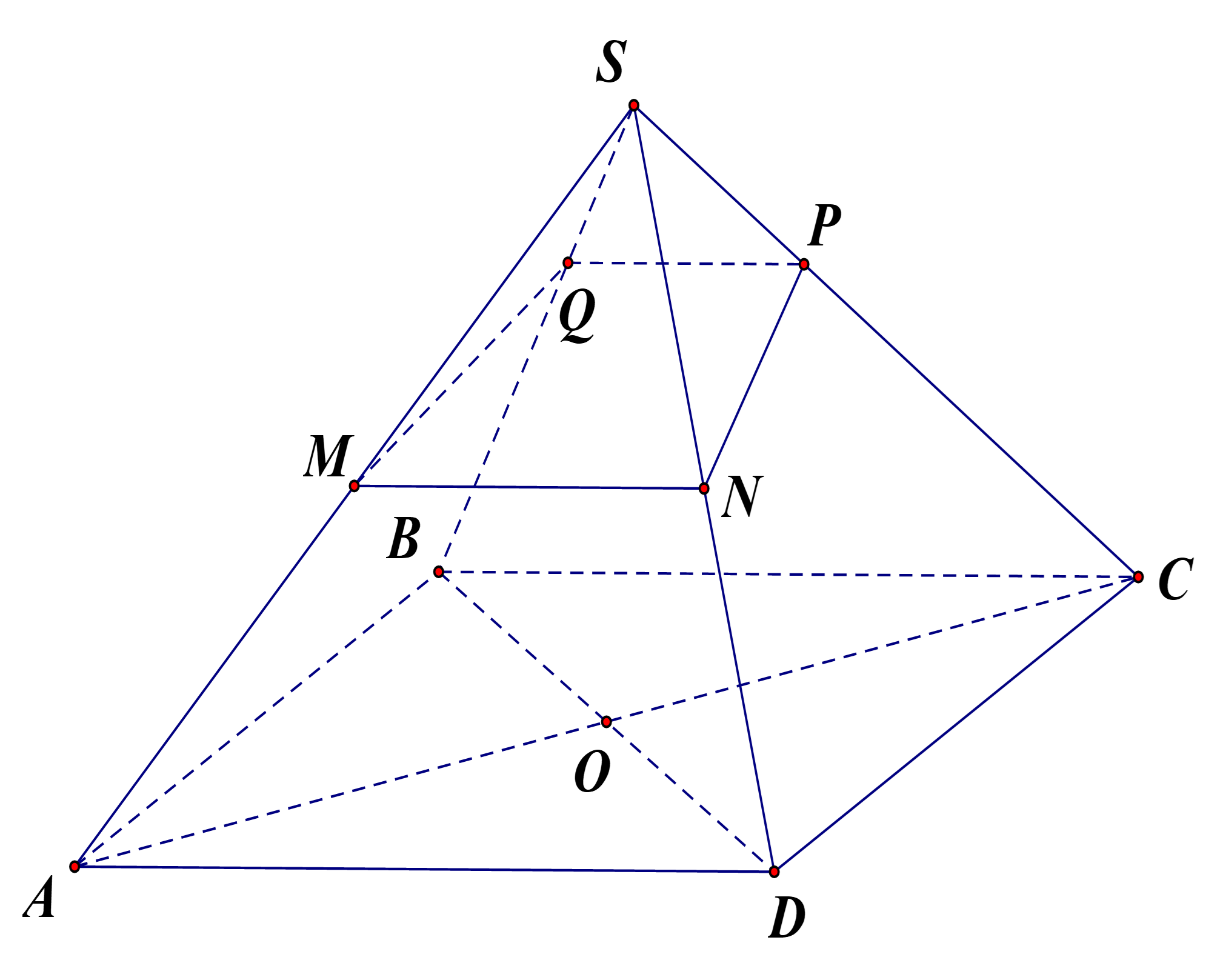
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD. Mặt phẳng ( alpha ) chứa MN cắt các cạnh SB, SC lần lượt tại (Q), (P). Đặt SQ/SB = x,
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA, SD. Mặt phẳng (α) chứa MN cắt các cạnh SB, SC lần lượt tại Q, P. Đặt SQSB=x, V1 là thể tích của khối chóp S.MNQP, V là thể tích của khối chóp S.ABCD. Tìm x để V1=12V.
A. x=−1+√334.
B. x=√2.
C. x=12.
D. x=−1+√414.