Cho hình chóp S.ABCD có cạnh bên SA tạo với đáy một góc 60 độ và SA = a căn bậc hai 3
72
02/05/2024
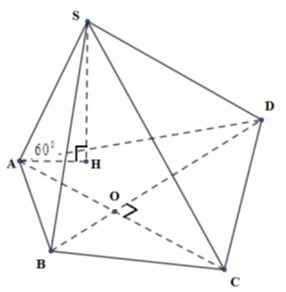
Cho hình chóp S.ABCD có cạnh bên SA tạo với đáy một góc \({60^0}\) và \(SA = a\sqrt 3 \), đáy là tứ giác có hai đường chéo vuông góc, \(AC = BD = 2a\). Tính thể tích V của khối chóp theo a.
A. \(V = \frac{{2{a^3}\sqrt 3 }}{3}\)
B. \(V = 3{a^3}\)
C. \(V = {a^3}\)
D. \(V = \frac{{3{a^3}}}{2}\)
Trả lời
Đáp án C
Phương pháp:
Diện tích tứ giác có 2 đường chéo vuông góc với nhau: \(S = \frac{1}{2}ab\) (a, b là độ dài 2 đường chéo)
Cách giải:
Gọi H là hình chiếu của S lên mặt phẳng đáy.
Tam giác SAH vuông tại H \( \Rightarrow SH = SA.\sin {60^0} = a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{3}{2}a\)
Diện tích đáy: \({S_{ABCD}} = \frac{1}{2}.AC.BD = \frac{1}{2}.2a.2a = 2{a^2}\)
Thể tích khối chóp: \({V_{S.ABCD}} = \frac{1}{3}.SH.{S_{ABCD}} = \frac{1}{3}.\frac{{3a}}{2}.2{a^2} = {a^3}\)
