Cho hình chóp S.ABC có góc ASB=CSB=60 độ, ASC= 90 độ và SA=SB=a, SC=3a
Cho hình chóp S.ABC có và . Tính thể tích V của khối chóp S.ABC
A.
B.
C.
D.
A.
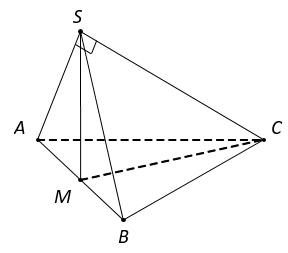
Tam giác SAC, có
Tam giác SBC, có
Tam giác ABC, có
Ta có vuông tại .
Từ và , ta có
Diện tích tam giác
Vậy thể tích khối chop Chọn D.
Cách 2.
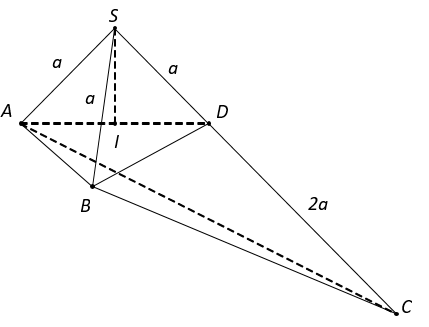
Trên cạnh SC lấy điểm D sao cho .
Dễ dàng suy ra
Ta tính được và
Suy ra
Ta có
Cách 3. Phương pháp trắc nghiệm. Cho hình chóp SS.ABC có và Khi đó ta có:
Áp dụng công thức, ta được