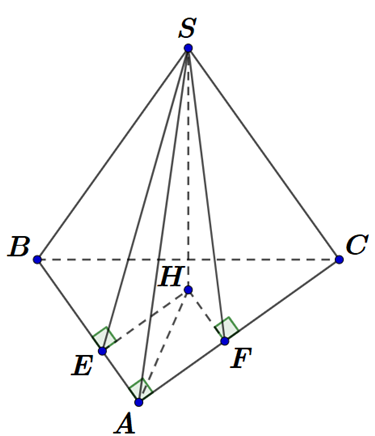
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và AB = căn bậc hai 3, AC = căn bậc hai 7, SA = 1. Hai mặt bên (SAB) và (SAC) lần lượt tạo với mặt đáy các góc bằng 45o và 60o. Thể tích của
37
09/06/2024
Cho hình chóp S.ABC có đáy là tam giác vuông tại A và , , SA = 1. Hai mặt bên (SAB) và (SAC) lần lượt tạo với mặt đáy các góc bằng 45o và 60o. Thể tích của khối chóp đã cho bằng
A.
B.
C.
D.
Trả lời
Chọn A
Gọi H là hình chiếu của S trên . Kẻ và .
Ta có
vuông cân .
Ta có
vuông nên .
Mà tứ giác HEAF là hình chữ nhật .
Ta có tam giác SHA vuông tại H .
Vậy .