Cho hàm số y = f(x) có đạo hàm trên R và f'(x) = (x - 1)(x + 2) với mọi x. Số các giá trị nguyên m sao cho hàm số y

A. 23

B. 27

C. 24

D. 26

Trả lời

Chọn C

Ta có:

$y=f\left(\left|2x^3+3x^2-12x-m\right|\right)\Rightarrow y^{\text{'}}=\frac{\left(2x^3+3x^2-12x-m\right)\left(6x^2+6x-12\right)}{\left|2x^3+3x^2-12x-m\right|}.f^{\text{'}}\left(\left|2x^3+3x^2-12x-m\right|\right)$

$f^{\text{'}}\left(x\right)=\left(x-1\right)\left(x+2\right)=0\iff \left[\begin{array}{l}x=1\\ x=-2\end{array}\right.$

Ta có: $y^{\text{'}}=0\iff \left[\begin{array}{l}6x^2+6x-12=0\\ \left|2x^3+3x^2-12x-m\right|=1\end{array}\right.$ và y' không xác định $2x^3+3x^2-12x-m=0$.

$6x^2+6x-12=0\iff \left[\begin{array}{l}x=1\\ x=-2\end{array}\right.$

Theo yêu cầu bài toán thì phương trình $2x^3+3x^2-12x-m=0$ và $\left|2x^3+3x^2-12x-m\right|=1$ phải có 9 nghiệm phân biệt.

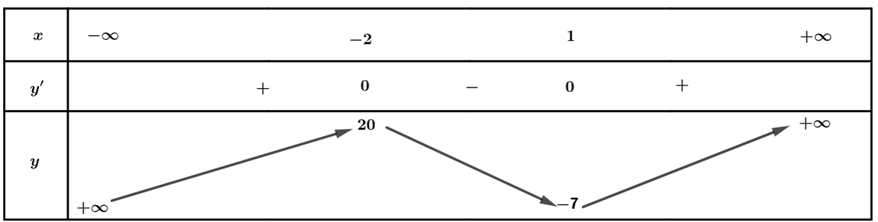
Khảo sát hàm số $y=2x^3+3x^2-12x$ ta có được bảng biến thiên:

Dựa vào bảng biến thiên: $\left[\begin{array}{l}2x^3+3x^2-12x=m\\ 2x^3+3x^2-12x=m+1\\ 2x^3+3x^2-12x=m-1\end{array}\right.$ có 9 nghiệm: $\left\{\begin{array}{l}m+1<20\\ m-1>-7\end{array}\right.\iff -6<m<19$

Vậy có 24 giá trị nguyên m thỏa mãn.