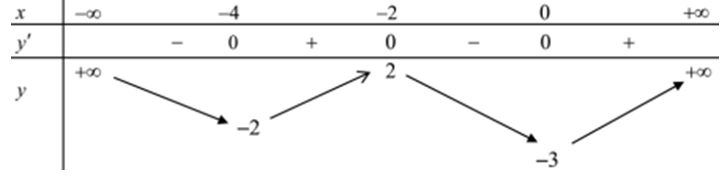
Cho hàm số y = f(x) có bảng biến thiên như sau: Có bao nhiêu giá trị nguyên của m để phương trình 4f(x2 - 4x) = m có ít nhất ba nghiệm dương phân biệt?
56
09/06/2024
Cho hàm số y = f(x) có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của m để phương trình 4f(x2 - 4x) = m có ít nhất ba nghiệm dương phân biệt?
A. 19
B. 21
C. 20
D. 18
Trả lời
Chọn C
Ta có: 4f(x2−4x)=m⇔4f(u(x))=m, với u(x)=x2−4x.
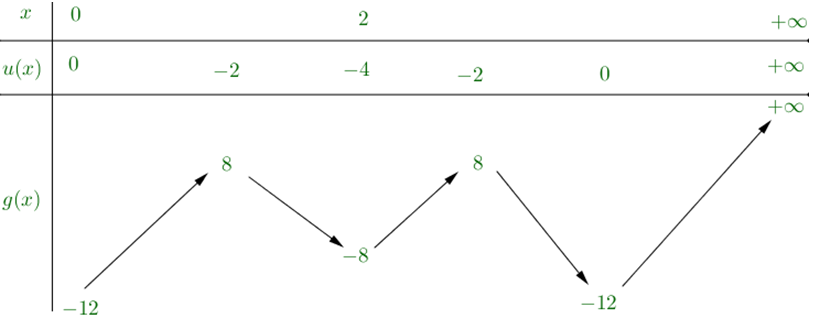
Đặt g(x)=4f(u(x)).
Phương trình đã cho có ít nhất ba nghiệm dương phân biệt khi đô thị hàm số y = g(x) trên khoảng (0 ; +∞) và đường thẳng y = m có ít nhất ba điểm chung phân biệt.
Vậy phương trình 4f(x2−4x)=m có ít nhất ba nghiệm dương phân biệt khi −12<m≤8, mà m nguyên nên m = -11, -10, ..., 8.