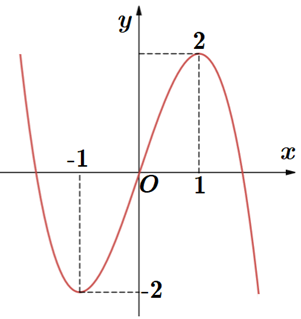
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong như hình vẽ bên.

Có bao giá trị nguyên của tham số $m\in \left[0;2023\right]$ để hàm số $y=\left|\frac{mf\left(x\right)+100}{f\left(x\right)+m}\right|$ có đúng 5 điểm cực trị?

Chọn A

Xét hàm số $g\left(x\right)=\frac{mf\left(x\right)+100}{f\left(x\right)+m}$

Ta có $g^{\text{'}}\left(x\right)=\frac{m^2-100}{{\left[f\left(x\right)+m\right]}^2}{f}^{\text{'}}\left(x\right)$

Với $m=\pm 10$ thì hàm số g(x) là hàm hằng nên $y=\left|g\left(x\right)\right|$ là hàm hằng nên loại $m=\pm 10$.

Với $m\ne \pm 10$, ta có $g^{\text{'}}\left(x\right)=0\iff f^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{c}x=1\\ x=-1\end{array}\right.$.

Do đó g(x) có hai điểm cực trị. Nên để hàm số $y=\left|g\left(x\right)\right|$ có đúng 5 điểm cực trị thì phương trình g(x) = 0 có ba nghiệm phân biệt <=> mf(x) + 10 = 0 có ba nghiệm phân biệt.

Với m = 0, phương trình vô nghiệm nên loại m = 0.

Với $m\ne 0$, phương trình $\iff f\left(x\right)=\frac{-100}{m}$.

Để $f\left(x\right)=\frac{-100}{m}$ có ba nghiệm $\iff -2<\frac{-100}{m}<2$, mà $m\in \left[0;2023\right]$ nên m > 50.

$\Rightarrow m\in \left\{51;52;\mathrm{...};2023\right\}$.