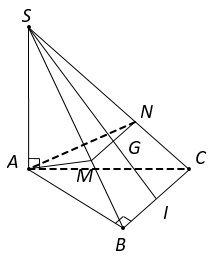
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, $AC=a\sqrt{2}$ , SA=a và vuông góc với đáy $\left(ABC\right)$ . Gọi G là trọng tâm tam giác SBC. Mặt phẳng $\left(\alpha \right)$  qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính theo a thể tích V của khối chóp S.AMN.

Từ giả thiết suy ra $AB=BC=a$ .