Cho hình chóp (S.ABC), (M)và (N) là các điểm thuộc các cạnh (SA) và (SB) sao cho (MA = 2SM), (SN = 2NB), ( alpha ) là mặt phẳng qua (MN) và song song với (SC). Mặt phẳng (alpha ) chia khối ch
38
01/05/2024
Cho hình chóp \(S.ABC\), \(M\)và \(N\) là các điểm thuộc các cạnh \(SA\) và \(SB\) sao cho \(MA = 2SM\), \(SN = 2NB\), \(\left( \alpha \right)\) là mặt phẳng qua \(MN\) và song song với \(SC\). Mặt phẳng \(\left( \alpha \right)\) chia khối chóp \(S.ABC\) thành hai khối đa diện \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\) với \(\left( {{H_1}} \right)\) là khối đa diện chứa điểm \(S\), \(\left( {{H_2}} \right)\) là khối đa diện chứa điểm \(A\). Gọi \({V_1}\) và \({V_2}\) lần lượt là thể tích của \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
A. \(\frac{4}{5}\).
B. \(\frac{5}{4}\).
C. \(\frac{3}{4}\).
D. \(\frac{4}{3}\).
Trả lời
Lời giải
Chọn A
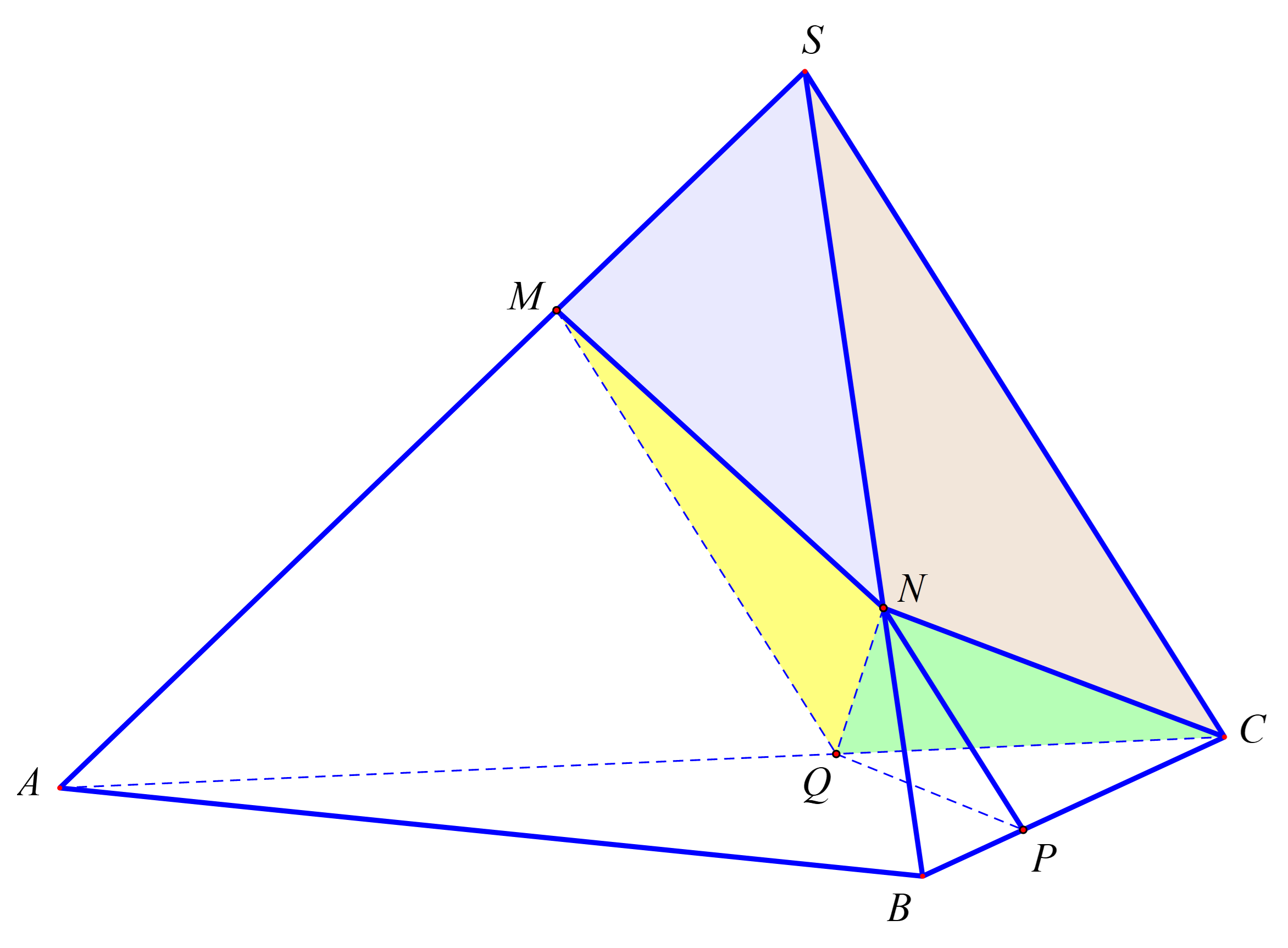
Kí hiệu \(V\) là thể tích khối tứ diện \(SABC\).
Gọi \(P\), \(Q\) lần lượt là giao điểm của \(\left( \alpha \right)\) với các đường thẳng \(BC\), \(AC\).
Ta có \(NP\;{\rm{//}}\;MQ\;{\rm{//}}\;SC\).
Khi chia khối \(\left( {{H_1}} \right)\) bởi mặt phẳng \(\left( {QNC} \right)\), ta được hai khối chóp \(N.SMQC\) và \(N.QPC\).
Ta có \(\frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} = \frac{{d\left( {N,\left( {SAC} \right)} \right)}}{{d\left( {B,\left( {SAC} \right)} \right)}} \cdot \frac{{{S_{SMQC}}}}{{{S_{SAC}}}}\).
\(\frac{{d\left( {N,\left( {SAC} \right)} \right)}}{{d\left( {B,\left( {SAC} \right)} \right)}} = \frac{{NS}}{{BS}} = \frac{2}{3}\); \(\frac{{{S_{AMQ}}}}{{{S_{ASC}}}} = \frac{{AM}}{{AS}}.\frac{{AQ}}{{AC}} = {\left( {\frac{{AM}}{{AS}}} \right)^2} = \frac{4}{9} \Rightarrow \frac{{{S_{SMQC}}}}{{{S_{ASC}}}} = \frac{5}{9}\).
Do đó \(\frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} = \frac{2}{3} \cdot \frac{5}{9} = \frac{{10}}{{27}}\).
\(\frac{{{V_{N.QPC}}}}{{{V_{S.ABC}}}} = \frac{{d\left( {N,\left( {QPC} \right)} \right)}}{{d\left( {S,\left( {ABC} \right)} \right)}} \cdot \frac{{{S_{QPC}}}}{{{S_{ABC}}}} = \frac{{NB}}{{SB}} \cdot \left( {\frac{{CQ}}{{CA}} \cdot \frac{{CP}}{{CB}}} \right) = \frac{1}{3} \cdot \left( {\frac{1}{3} \cdot \frac{2}{3}} \right) = \frac{2}{{27}}\).
Do đó \(\frac{{{V_1}}}{V} = \frac{{{V_{N.SMQC}}}}{{{V_{B.ASC}}}} + \frac{{{V_{N.QPC}}}}{{{V_{S.ABC}}}} = \frac{{10}}{{27}} + \frac{2}{{27}} = \frac{4}{9} \Rightarrow \frac{{{V_1}}}{{{V_1} + {V_2}}} = \frac{4}{9} \Rightarrow 5{V_1} = 4{V_2} \Rightarrow \frac{{{V_1}}}{{{V_2}}} = \frac{4}{5}\).
